«Теория систем и системный анализ»

И. Б. Родионов

↑	Оглавление
←	Лекция 6, «Информационное описание и моделирования систем»	Лекция 8, «Структура системного анализа»	→

Лекция 7: Основы теоретико-множественного описания и анализа систем

Система объекта

Объектом познания является часть реального мира, которая выделяется и воспринимается как единое целое в течение длительного времени. Объект может быть материальным и абстрактным, естественным и искусственным. Реально объект обладает бесконечным набором свойств различной природы. Практически в процессе познания взаимодействие осуществляется с ограниченным множеством свойств, лежащих в приделах возможности их восприятия и необходимости для цели познания. Система объекта задаётся на множестве отобранных для наблюдения свойств. Процедура задания системы включает ряд операций: назначение переменных, параметров и канала наблюдения.

Каждому свойству объекта назначается переменная, с помощью которой суммируется изменение проявлений свойства. Множеству наблюдаемых проявлений свойства ставится в соответствие множество значений переменной.

D: S_i = [S_i,j, j={1,N}] → X_i = [X_i,j,j={1,N}],

где S_i — i-ое свойство, X_i — переменная.

Процедура наблюдения свойств объекта включает базу и канал наблюдения. Под базой наблюдения понимается признаки различения одного проявления свойства от другого. Типовыми базами являются время, пространство, группа и их комбинации. Операционное выражение базы будем познавать параметром наблюдения. Операцию назначения значению параметра значения переменной назовём каналом наблюдения. В этом смысле необходимо различать чёткий и нечёткий канал наблюдения. Чёткий канал назначает одному значению параметра одно значение переменной. В этом случае система задаётся на чётком множестве значений переменных. В нечётном канале наблюдения не существует однозначного решения о том, какое значение переменной назначить определённому значению параметра. Поэтому система задаётся в виде нечётких множеств состояний переменных.

Формально система может быть представлена в виде множества:

S = (X, T, R, Z),

где X — множество переменных, T — множество параметров, R — отношения на множества X и T, Z — цель исследований.

Отношения между переменными и параметрами здесь понимаются в самом широком смысле, включая как ограничение, сцепление, соединение и т.д. В дальнейшем изложении материала смысл отношений будет ограничен понятиями следующего вида:

1. Отношения эквивалентности, имеющее смысл «соседства» значений переменных системы на полном множестве состояний;

   X_1,j, X_2,p, ..., X_k,c ∈ C1

   где X_k,n — значение k-ой переменной.

2. Отношения упорядоченности переменных по роли, вкладу и т. д в достижение цели

   C2 ⊂ X×X

3. Отношения упорядоченности переменных на множестве параметров

   D ⊂ X×T

4. Отношения упорядоченности вида

   Э ⊂ C1×C2×D

Эти виды отношения отражают соответственно структурные (C₁,C₂), динамические (X) и интегративные свойства системы (Э), которые объединяют структурные и динамические (качество, эффективность, безопасность, живучесть и т.д.).

Структура системы

Под структурой системы понимается устойчивое множество отношений, которое сохраняется длительное время неизменным, по крайней мере в течение интервала наблюдения. Структура системы опережает определенный уровень сложности по составу отношений на множестве переменных и их значений или что эквивалентно, уровень разнообразий проявлений объекта.

Для приведенных уровней разнообразия справедливо соотношение S4CS3CS2CS1.

Формально структура представляет упорядоченности переменных и их значений по некоторому заданному относительно цели фактору. Физически (если такая интерпретация возможна) структура представляет аналитические и функциональные связи между элементами системы.

Полное множество состояний системы

В системе заданной на множестве переменных X = [X_n, i={1,N}], каждая переменная изменяет свое значение в некоторой области значений заданной множеством физически различных значений X_n ={1,N}[X_n,k, k={1,N}]. Зафиксированное значение всех переменных относительно одного значения параметра представляет вектор состояния системы

C_i = [α_1,k1, X_2,k2, ..., X_N, k_N]

Множество всех возможных векторов состояний C = [C_i , i={1,|C|}], образует полное множество состояний, где |C| = ∏k_n

Реально состояние системы не равнозначны. Одни более, другие менее предпочтительны, другие запрещены. Это обстоятельство задается в виде функции ограничения.

Функция ограничения на полном множестве состояния

Состояние системы на полном множестве состояний неравнозначны. Одни состояние более другие менее предпочтительны, третьи практически не осуществлены. Неравнозначность состояния задается в виде функции ограничения. В общем случае она представляет собой отображение полного множества состояний:

f₀: C → P,

где Р — заданное множество.

Предположим, что на множестве интервалов наблюдений объекта для функции ограничения справедливо условие:

f₀ = 1, если с ⊂ C^,

f₀ = 0, если с П ¬_in; C^,

где с — вектор состояния системы, C^ — подмножество полного множества состояний.

В этом случае функция ограничения образует замкнутое множество состояний C^. Такие системы будем называть замкнутыми. В обратном случае, когда от интервала к интервалу наблюдения состав элементов C^ меняется, т.е. функция ограничена для интервалов наблюдений, f₀ⁱ ≠ f₀^j не множественны, то система будет разомкнутой.

Рассмотрим отображение в интервале наблюдения Т множества моментов времени измерений примененных на множестве наблюдаемых состояний C^.

f₀ : C^ → Т, Т → C^

Здесь возможны два случая. В одном отображение однозначно, в другим — многозначно.

В случае однозначного отображения, т.е. когда одному значению времени соответствует только одно состояние системы, последняя будет детерминированной. Если отображение многозначно, т.е. одному значению времени допускается два и более состояний, то система будет стохастической.

Для детерминированной системы функция ограничения имеет вид:

f₀ = 1, если при t = t_i, C = C_i

f₀ = 0, если при t = t_i, C ≠ C_i

У стохастической системы в момент наблюдения t = t_i состояние системы С ∈ C^ является случайным. Ограничение полного множества состояний системы в этом случае задается нечеткими функциями типа вероятности, возможности, правдоподобности и др. В общем случае они представляют отображения вида:

f₀ : |С| → [0,1]

При выборе функции ограничения исходят из соотношения мощности полного множества состояний |С| и мощности множества моментов наблюдения |Т|. Если |С| ≤ |Т|, то предпочтительной является функция вероятности. В обратном случае |С| ≥ |Т|, предпочтительней функция возможностей.

Функция вероятности задается в следующем виде:

Р = [P_t , t = {1,|T|}],

где P_t< = N_k/∑N_k

N_k — число наблюдаемых состояний C_k.

|Т| = ∑N_k — общее число наблюдений

Функция возможности определяется следующим образом:

W = [W_k, k={1,k}]

Где W_k = N_k/max N_i, i ∈ |С|

Из приведенных формул видно, что в первом случае наблюденное число состояний системы C_k нормируется относительно общего числа наблюдения |Т|, во втором относительное число состояний с наибольшим значением.

Ck	О1	О2	О3	Nk	Pk	Wk1
1	0	0	0	10	0-1	0,532
2	0	0	1	5	0,05	0,173
3	0	1	0	20	0,2	0,164
4	0	1	1	5	0,05	0,175
5	1	0	0	0	0	06
6	1	0	1	30	0,3	1,07
7	1	1	0	10	0,1	0,338
8	1	1	1	20	0,2	0,61
				∑Nk=100	∑Pk=1	SWk≠1

Мера нечеткости множества состояний системы

У стохастических систем полное множество состояния с позиции их допустимости представляет собой нечеткое множество.

При этом уровень нечеткости может меняться в значительных приделах. Например, если вероятности состояний P(C_i) = P(C_j) равны, то он максимальный, а при уровне P(C_i) = 1 он минимален. Поэтому естественно надо ввести меру нечеткости полного множества состояний уровня нечеткости.

Для вероятностных систем нечетность задается через множество вероятностей состояния системы в виде отображения

H : P → [0, ∞]

В качестве меры уровня нечеткости принята энтропия [ ]. Она определяется по формуле:

H = −∑p(C_i)log_p(C_i)

Из этой формулы видно, что если p(C_i) = 1, то Н = 0, при p(C_i) = 1/|C| H = log₂|C|.

Таким образом, величина энтропии монотонно меняется в пределах:

0 ≤ Н ≤ log₂|C|

Для систем с поперечным множеством состояний можно ввести нормированную энтропию:

H^ = H/log₂|C|

Ее величина меняется в области значений

0 ≤ Н^ ≤ 1

Для возможностных систем аналогично нечеткость вводится через множество возможностей. А мера уровня нечеткости через возможностную энтропию. С формулами расчета этой энтропии можно познакомиться в работе [ ].

Рассмотрим систему на множестве интервалов наблюдения [T₁, T₂, T₃, ...]. В этом случае возможно, что от интервала наблюдения H_i = H_j, уменьшает [H₁ > H₂ > H₃ > ...] или возрастает [H₁ < H₂ < H₃ < ...]. В зависимости от характера интервалов энтропии на множестве интервалов наблюдения различают системы:

• закрытые, если [H₁ < H₂ < H₃ < ...]
• открытые, если [H₁ ≥ H₂ ≥ H₃ ≥ ...]

Системная сложность

Системная сложность рассматривается как условие для системных задач в виде предпочтения на множестве вариантов систем объекта. Мера системной сложности в этом смысле представляет размерность варианта задачи, по которой определяется временная и пространственная функция сложности алгоритма решения задачи, придел практической разрешимости задачи.

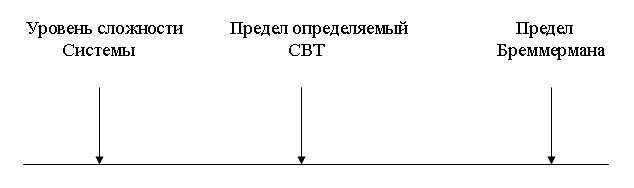
Анализ системной сложности должен дать ответ на следующие фундаментальные вопросы. Во-первых, о разрешимости. Если задача неразрешима, то необходимо ее переформулировка. Во-вторых, следует определить класс сложности задачи. Класс сложности задачи можно определить следующим показателями: приделом Бремермана, приделом возможностей вычислительной техники, приделом сложности варианта системы объекта.

Предел Бремермана

Для решения системной задачи данные о системе объекта необходимо физически закодировать. Общим способом кодирования данных является их представление в виде энергетических уровней величиной ΔЕ энергии решения системной задачи данные о системе объекта Е, которой мы располагаем. Число энергетических уровней согласно принципу в этом случае будет равно N = E/ΔE. Максимальное число физически разрешимых уровней для заданного количества энергии определяется неопределенности Гейзенберга. Согласно этого принципа величина уровня должна удовлетворять условию ΔE•Δt ≥ h, где Δt — длительность интервала наблюдения h = 6•6,25•10^-27 эрг/c — постоянная Планка. Из этого следует:

N ≥ E•Δt/h

Тогда с учетом формулы Энштейна Е = mc₂ (где с = 3•10¹⁰ см/c — скорость света, m — количество массы), получим:

N = mc₂•Δt/h

Отсюда следует, что измеритель массой 1 г за время 1 сек может обработать не более N = 1,36•10⁴⁷ бит данных.

Представим гипотетический измеритель массой равной массе Земли m = 6•1027 г. Этот измеритель за время равное времени существования Земли q 10 лет смог бы обработать порядка 10⁹³ бит данных. Это число обычно называют пределом Бреммермана.

Вычислительная сложность задачи

Предел Бреммермана дает оценку сложности задачи с точки зрения объекта данных, который необходимо обработать для решения задачи. Однако возможны условия, при которых задача может находиться за пределом Бреммермана, но практически неразрешимой. Причиной этого является размерность временной и пространственной функцией вычисления, под которым понимается соответственно время и объект памяти ЭВМ, которые необходимы для реализации алгоритма.

Разбор этих вопросов выходит за пределы нашего предмета и рассматривается в общей теории алгоритмов.

Мера сложности системы

Понятие «сложность объекта» как части внешнего мира (окружающей среды) широко используется в философии и естествознании. Следует различать две модификации сложности: (когда свойства целого сводится к сумме свойств составных элементов) и неоддитивную сложность-целостность, свойство которой не сводится к сумме свойств ее элементов. Та или другая модификация используется в зависимости от условий и задачи. Соответственно разработаны два основных принципа оценки сложности. В основе первого лежит оценка объекта информации необходимой для описания системы объекта. В основе второго — объекта информации необходимой для разрешения нечеткости (неопределенности) системы.

Описание аддитивной или иначе дескриптивной сложности сводится к оценке числа элементов системы, их состояний и отношений между ними. Информация необходимая для списания этой модификации сложности понимается в синтаксическом смысле. Поэтому эту модификацию иначе называют дескриптивная сложность. Мера дескриптивной сложности I(X₁) должно удовлетворять следующим условиям

1. I(ф) = 0
2. Если X₁ ⊂ X₂, то I(X₁) < I(X₂)
3. Если X₁ и X₂ изоморфны, то I(X₁) = I(X₂)
4. Если X₁ ∩ X₂ = ∅,то I(X₁ ∩ X₂) = I(X₁)+I(X₂)

Дескриптивная мера сложности обеспечивает потребности решение системных задач, объектом которых являются детерменированные системы. Однако в классе недертеминированных систем эта мера сложности уже неприемлема, так как она не позволяет учесть сложность, которую вносит нечеткость стохастической системы. В этом случае необходимо использовать другой принцип оценки сложности в виде объема информации необходимого для разрешения нечеткости полного множества состояний. Здесь также имеется в виду синтаксическая информация. Однако оценка ее объекта основывается на мерах нечеткости. Сложность систем с этой позиции изучалась с разных сторон. Однако наиболее конструктивными представляются результаты, полученные в теории информации.

В теории информации достаточно хорошо разработан механизм оценки сложности вероятностных систем на основе статистической меры количества информации предложенной К.Шенноном. Здесь за количество информации необходимого для описания системы принимается величина равная энтропии системы. Рассмотрим ряд важных энтропийных оценок сложности на принципе решения задач.

1. Пусть система S содержит N переменных, каждая переменная имеет К состояний, и пусть все состояния системы равновероятны. У такой системы мощность полного множества состояний равна |C| = k^N, вероятностная функция ограничений имеет вид P = {P_i = P_j = 1/k^N}. В этом случае энтропия будет равна

H = N•log(K)

Нетрудно видеть следующее. Для систем S(N₁,K) и S(N₂,K), если N₁ > N₂, то H₁ > H₂, для системы S(N₁+N₂,K), H = H₁+H₂.Для систем S(N,K₂), если K₁ > K₂, то H₁ > H₂.

Из этого следует, что энтропийная мера сложности обладает всеми свойствами дискриптивной сложности.

2. Пусть даны системы S₁, S₂, S₃, состоящие из одной переменной с двумя состояниями, т.е. К=1, N=2. Вероятностные функции ограничения полного множества состояний соответственно имеют вид P₁=(P₁=0,2, P₂=0,2), P₂=(P₁=0,5, P₂=0,5), P₃=(P₂=0,7, P₂=0,3).

На рис. показаны значения энтропий для этих систем.

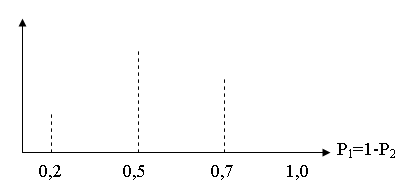
Как видим три системы, обладающие одинаковым множеством элементов и состояний, имеют разные уровни энтропийной сложности. Следовательно, энтропийная мера сложности учитывает количественные свойства элементов, что не позволяет сделать дескриптивное.

Классы систем

Методы упрощения систем

В ходе решения системных задач по разным причинам могут возникать потребности упрощения системы. Такими причинами являются сложность физической интерпретации результатов решения задачи, малый объем наблюдений или недостаточные вычислительные и временные ресурсы.

Известно два основных подхода к упрощению систем: сокращение множества переменных и объединение состояний системы в классы эквивалентности.

В общем виде задача упрощения состоит в следующем. Для системы заданной на множестве переменных X с полным множеством состояний С необходимо найти вариант упрощенной системы на подмножестве переменных X' ⊂ X или подмножестве состояний C' ⊂ C.

При исключении переменных общее число возможных вариантов упрощения равно

Л_X = 2^|X| - 2

Рассмотрим систему из трех переменных X₁, X₂, X₃. Варианты упрощения системы путем исключения переменных приведены на рис.

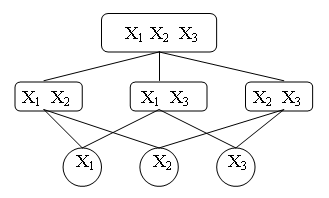
Рис. — Упрощение системы путем исключения переменных

При объединении состояний системы в классы эквивалентности общее число вариантов упрощения равно

Л_C = ∑Лⁱ_|C|

Целью упрощения является смещение уровня сложности системы при сохранении минимума нечеткости. Оба эти условия противоречивы. Поэтому выбор подходящего варианта необходимо производить по близости функций ограничения на полном множестве состояний исходной и упрощенной систем.

Рассмотрим функцию ограничения упрощенной системы. Пусть Х и X₁ ⊂ X', f и f' соответственно множество переменных и функции ограничения на множестве состояний исходной и упрощенной системы. Полное множество состояний С' упрощенной системы есть проекция вида

C' = Пр_X'•C

Поэтому функция ограничения f ' также является проекцией

f' = Пр_Х•f

Рассмотрим пример. Пусть дана система на множестве переменных X₁, X₂, X₃, X₄.В таблице приведено полное множество состояний и значение функций ограничения. Выберем вариант упрощения (X₁ X₂ X₃ X₄) → (X₁ X₂). У упрощенной системы состояние C_i включает состояния C₁, C₂, C₃ исходной системы, состояние C'₂ состояния C₄, C₅, C'₃ состояния C₆, C₇, C₈.

Ci X1 X2 X3 X4 fi 1 0 0 0 0 0,2 2 0 0 0 1 0,2 3 0 0 1 0 0,1 4 0 1 0 0 0,1 5 1 0 0 0 0,1 6 0 1 0 1 0,1 7 1 0 0 1 0,1 8 1 0 1 0 0,1

C' X1 X2 f'i 1 0 0 0,2+0,2+0,1=0,52 2 0 1 0,1+0,1=0,23 3 1 0 0,1+0,1+0,1=0,34

Полное множество состояний упрощенной системы и значение функции ограничения приведены в табл.

Аналогичным образом может быть найдена функция ограничения в случае упрощения путем объединения состояний системы в классы эквивалентности.

Близости функций ограничения может быть выражена через метрическое расстояние между ними. Существует много разных типов метрический расстояний. Поэтому ограничимся рассмотрением двух следующих модификаций.

Класс расстояний Минковского определяется следующей формулой [].

Структурированная система.

Структурирование системы заданной на множестве переменных Х представляет собой разделение исходного множества переменных на подмножества Xⁱ ⊂ X. Подмножество структурированной системы будет называть подсистемами структурированной системы.

Подмножество структурированной системы должны удовлетворять следующим условиям.

1. Все подмножества задаются на одном параметрическом множестве.

2. Каждое подмножество Хⁱ имеет общие переменные хотя бы с одним подмножеством т.е. справедливо следующее

   X¹ ∩ (X₂ ∪ X₃ ∪ X^m) ≠ ∅

   X² ∩ (X₁ ∪ X₃ ∪ X^m) ≠ ∅

   _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

   X^m ∩ (X₁ ∪ X₂ ∪ X^m-1) ≠ ∅

Имеет ряд причин требующих представления системы в виде структурированной. Во-первых нередко формирование системы происходит на множествах наблюдений полученных в разное время и в разных местах. Во-вторых должным образом обоснованная структурированная система может выявлять свойства, которые в явном виде не проявляются в исходной системы. В-третьих высокий уровень сложности системы может потребовать исследования системы по частям. Отсюда вытекают две возможные задачи:

1. Заданы системы на множество [X¹, X², X³, ...]. Требуется сформировать структурированную систему и найти соответствующую исходную систему на множестве X = [X¹ ∪ X² ∪ α³ ∪ ...].
2. Задана система. Требуется найти структурированную систему, которая выявляет равные свойства.

Любая система может иметь множество соответствующих ей структурированных систем.

Пример. Задана система на множестве X = (X₁, X₂, X₃). Соответствующие ей варианты структурированных систем приведены на рис.

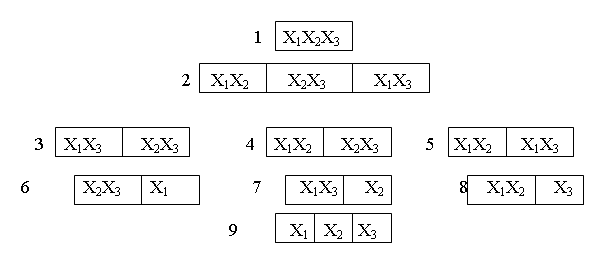
В этом множестве вариантов как видно не все удовлетворяют условиям структуризации (6,7,8,9).

Поэтому очевидно, что возникает вопрос, какой вариант структуризации наилучшим образом представляет заданную систему. Здесь возможны различные подходы. В самом общем виде условие выбора варианта можно сформулировать так. Лучшим вариантом структурированной системы является тот, который использует всю информацию исходной системы и не содержит ни какой другой.

Для систем, у которых определена функция поведения, это условие можно определить как принцип максимума нечетности. Конкретно для систем с вероятностной функцией поведение это принцип максимума энтропии т.е. лучший вариант структурированной системы обладает наибольшей величиной нечеткости или энтропии.

Однако в практических задачах нередко условие может потребовать минимизировать ошибку выбора варианта структуризации. Это условие можно сформулировать, как принцип минимального риска. В его основе лежит сравнение вариантов структуризации по близости функций поведения исходной и структуированной системы.

В ряде работ оценку близости функций поведения двух систем предлагается производить на основе класс метрических расстояний Минковского

d (f₁, f₂) = ∑ [f₁(d_k) - f₂(d_k)]^1/p

Функция ограничения полного множества состояний структурированной системы.

Пусть для исходной системы S = (X, T, C, Z) сформирована структурированная система S' = [(X¹, X², ..., Xm), T, Z], где Xⁱ ⊂ X. Каждую подсистему заданную на подмножестве αⁱ можно рассматривать как вариант упрощения исходной путем исключения переменных. Тогда если исходная система имеет функцию ограничения f, то подсистема будет иметь функцию ограничения вида

fⁱ = Пр_Xⁱ f

Это соотношение можно конкретизировать исходная система S имеет полное множество состояний С = (Ck, k=1,k), а каждая подсистема Sⁱ структуированной системы Cⁱ М C, тогда для значений fⁱ и f

f'(CX) = f(Ck)

Пример. Дана система S' с переменными a₁, a₂, a₃ и функцией поведения f_n.Найти функции поведения подсистем S₁ и S₂ c переменными соответственно a₁, a₂ и a₂, a₃.

dk a1 a2 a3 fn(dk) 1 0 0 0   2 0 0 1   3 0 1 0   4 0 1 1   5 1 0 0   6 1 0 1   7 1 1 0   8 1 1 1	d'k a1 a2 f'   0 0 fn(1)+fn(2)=   0 1 fn(3)+fn(4)=   1 0 fn(5)+fn(6)=   1 1 fn(7)+fn(8)
	d''k a2 a3 f'' 1 0 0 fn(1)+fn(5)= 2 0 1 fn(2)+fn(6)= 3 1 0 fn(3)+fn(7)= 4 1 1 fn(4)+fn(8)=

Пример. Даны три системы S₁, S₂, S₃ с переменными (a₁, a₂), (a₂, a₃), (a₁,a₃) с функциями поведения f_n', f_n'', f_n'''. Найти функцию поведения f_n системы S с переменными (a₁ a₂ a₃).

Из уравнения f^X(d) = ∑ f(d) следует система уравнений

d' a1 a2 fn'   0 0 0,4   0 1 0,3   1 0 0,2   1 1 0,1	d'' a2 a3 fn''   0 0 0,4   0 1 0,2   1 0 0,1   1 1 0,3	d''' a1 a3 fn'''   0 0 0,4   0 1 0,3   1 0 0,1   1 1 0,2
1. fn'(1) = fn(1) + fn(2) 2. fn'(2) = fn(3) + fn(4) 3. fn'(3) = fn(5) + fn(6) 4. fn'(4) = fn(7) + fn(8)	5. fn''(1) = fn(1) + fn(5) 6. fn''(2) = 7. fn''(3) = 8. fn''(4) =	9. fn'''(1) = 10. fn'''(2) = 11. fn'''(3) = 12. fn'''(4) =

Подставим в систему уравнений исходные данные для f^X(d) и учитывая ограничения

0 ≤ f_n(d) ≤ 1

Получим решение в виде неравенства

0,3 ≤ f_n(1) ≤ 0,4

Пример. Этот пример содержит описание исследования политической ситуации и уровня цен на бирже США.

• a₁ — политическая партия президента. Демократическая-0. Республиканская-1.
• a₂ — Большинство в палате представителей. Демократическая-0. Республиканская-1.
• a₃ — Большинство в сенате. Демократическая-0. Республиканская-1.
• a₄ — Уровень цен на бирже. Падает-0. Растет-1

Данные наблюдения регистрировались в период 1897—1921г. каждые 4 года т.е. в 21 интервале. Результаты наблюдения приведены в таблице.

Поскольку имеется 21 наблюдение и 16 состояний системы, т.о. ограничение на множество состояний задается в виде функций распределения возможностей

d1	a1	a2	a3	a4	N(dk)	f(dk)=N(dk)/maxn(dk)
1	0	0	0	0	6	1,0
2	1	0	0	0	2	0,33
3	0	0	0	1	4	0,66
4	1	1	0	1	1	0,165
5	0	1	1	1	1	0,165
6	1	1	1	0	1	0,165
7	1	1	1	1	6	1,0

Варианты структурированных систем приведены в таблице в порядке возрастания меры расстояния δ = ∑ (f(d_k)-f_C(d_k))^1/p, где f_C(d_k) функции поведения структурированной системы.

N		δ
1	123/134, 123/13/124/14 124/13	0,00072
2	123/13/124	0,01383
3	123/124/3	0,02774
4	124/3/23	0,03335
5	12/3/23/24	0,05796
6	1/3/23/24, 12/3/23/4	0,16677
7	1/3/23/4	0,28058
8	1/23/4	0,41389
9	1/2/3/4	0,5610

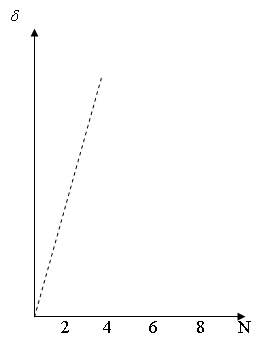
Интерпретация результатов решение задачи состоит в следующем. Из графика зависимости меры расстояния δ(f,f_C) от варианта структуризации видно, что он имеет характерную точку N=5. Структуированная система для варианта N=5 приведена ниже.

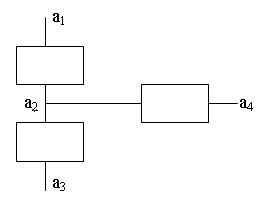
Из рисунка видно переменная a₂ является связующим звеном системы т.е. фактором определяющим цены на бирже в наибольшей степени.

Характеристическая функция

В системных задачах цель системы находится «в руках» пользователя. Это значит, что с позиции системных свойств цель представляет предпочтительное для пользователя ограничение свойств системы. Из этого следует, что система может рассматриваться относительно любой цели. И любая система в какой-то степени соответствует цели.

Близость действительных и желаемых свойств называется характеристикой системы относительно цели или просто характеристической функцией.

Пусть S множество систем, отличающихся свойствами, которые определяют понятия цели. Характеристическую функцию системы можно представить следующим образом

ω : S × S → [0,1]

Это отображение удобно определить с помощью функции расстояния

ω(S, S₉) = 1 - [δ(S, S_k)]/max_kδ(S, S_k)

где S, S_k, S₉ S , max_kδ(S, S_k) — максимальное расстояние на множестве S×S.

Используя понятия характеристической функции введем понятие целенаправленной системы. Система S может рассматриваться как целенаправленная относительно заданной цели S₉, если ее характеристика больше заданного порога

ω(S, S₉) ≥ ω₀

Рассмотрим следующую задачу. Предложим, что цель определена с помощью функции поведения f* на множестве систем S = (S₁, S₂, ..., S_m) и для них определены функции поведения F = (f₁, f₂, ..., f_m).

Расстояние между системами определяется следующим образом

δ(f_i, f*) = ∑ [f_i(d_k) - f*(d_k)]^1/p

где d_k ∈ D — множество состояний системы.

K = |D| — мощность множества состояний.

Пусть система некоторого вычислительного комплекса задана на трех переменных X₁, X₂, X₃ представляющих состояние трех устройств комплекса: X_i = 0, если в момент наблюдения устройство не работает и X_i = 1 в обратном случае.

а)	б)	в)	г)
X1 X2 X3 f1 0 0 1 0,15 0 1 0 0,2 1 0 0 0,1 1 1 0 0,25 1 1 1 0,3	X1 α2 X3 X4 f 0 1 1 1 0,1 1 0 0 0 0,02 1 0 1 0 0,03 1 1 0 0 0,04 1 1 0 1 0,01 1 1 1 0 0,25 1 1 1 1 0,55	X1 X2 X3 f2 0 1 1 0,1 1 0 0 0,02 1 0 1 0,03 1 1 0 0,05 1 1 1 0,8	f1* f2* f3* 0 0 0,2 0 0 0,2 0 0 0,2 0 0,5 0,2 1 0,5 0,2

Пусть система некоторого вычислительного комплекса задана на трех переменных a₁, a₂, a₃, представляющих состояния трех его устройств: a_i = 1 если в момент наблюдения устройство работало, a_i = 0 в обратном случае.

a1	a2	a3	f1	a1	a2	a3	a4	f	a1	a2	a3	f2	f1*	f2*	f3*
0	0	1	0,15	0	1	1	1	0,1	0	1	1	0,1	0	0	0,2
0	1	0	0,2	1	0	0	0	0,02	1	0	0	0,02	0	0	0,2
1	0	0	0,1	1	0	1	0	0,03	1	0	1	0,03	0	0	0,2
1	1	0	0,25	1	1	0	0	0,04	1	1	0	0,05	0	0,5	0,2
1	1	1	0,3	1	1	0	1	0,01	1	1	1	0,8	1	0	0,2
				1	1	1	0	0,25
				1	1	1	1	0,55

Множество состояний этой системы и функция поведения приведены в таблице а). Добавим к комплексу еще одно устройство, которое представлено переменной X₄. Множество состояний новой системы состоящей из четырех переменных (X₁, X₂, X₄) и ее функция поведения представлены в таблице б). Используя понятие структурированной системы, найдем для подсистемы Sn=(X₁ X₂ X₃) системы S=(X₁ X₂ X₃ X₄) функцию поведения по формуле

f(d_k) = f(dx)

Ее значение приведено в таблице в). В таблице г) приведены три целевых функции f₁*, f₂*, f₃*.

Теперь найдем характеристические функции системы S=(X₁ X₂ X₃) относительно целевой функции поведения f₁*, f₂*, f₃*. Они имеют значения

ω(f₁, f₁*) = 0,3; ω(f₁, f₂*) = 0,55; ω(f₁, f₃*) = 0,85.

И для системы S = (X₁ X₂ X₃ X₄). Они имеют соответственно следующие значения

ω(f₂, f₁*) = 0,8; ω(f₂, f₂*) = 0,55; ω(f₂, f₃*) = 0,27.

Сравнивая изменения значение функции за счет добавлений переменной X₄

Δω_i = ω(f₂, fⁱ*)  — ω(f₁, fⁱ*)

Получим соответственно значения Δω₁ = 0,5, Δω₂ = 0 и Δω₃ = -0,58. Эти значения показывают следующее. Относительно цели f₁* переменная X₄ является переменной выбора цели, относительно f₂* не является переменной выбора цели и для цели f₃* является переменной уклонения от цели.

Таким образом, приведенный пример показывает, что введенное понятие характеристической функции системы представляет собой инструмент системного анализа, который позволяет решить задачи оценки целенаправленности систем и оценки роли, переменных в обеспечении целенаправленности.

Динамическая система

Динамическая система представляет математическую модель функционирования объекта анализа в пространстве и времени. Чтобы модель охватила широкий класс реальных объектов необходимо исходить из самых общих предположений о характере объекта. Поэтому система определяется в терминах наблюдаемых свойств и взаимосвязи между ними.

Под процессом функционирования понимается изменение состояния системы под действием внутренних и внешних причин. При этом состояние системы в фиксированный момент времени представляет вектор наблюденных значений переменных (проявлений свойств).

Определим динамическую систему в виде отношения на множествах X, Y, T, C.

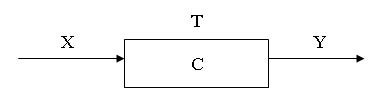
Множества X и Y представляет воздействия на систему внешней среды и ее реакции. Далее будем их называть входными и выходными переменными. Множество Т представляет множество [t₀, t₁, t₂, ...] множеств времени в интервале наблюдения.

Z_i = <a₁, m₁, a₂, m₂, ..., a_N, m_N>

Полное множество состояний системы образует фазовое пространство состояний динамической системы. Изменение состояния системы это переход из одной точки фазового пространства Cⁱ в другую C_j. Он происходит под воздействием входных сигналов X_k ⊂ X. Процесс переходов Cⁱ → C^j → C_c → ... → C_p происходит во времени.

Рассмотрим процесс переходов системы в фазовом пространстве состояний.

Пусть в начальный момент наблюдения t₀ система находилась в некотором состоянии, который будем называть начальное состояние C_t0. Множество всех возможных начальных состояний есть декартовое произведение t₀ × C. Множество всех возможных входных сигналов в моменты времени t₁, t₂, ... тоже есть декартово произведение Т × Х.

Множество всех возможных переходов системы в интервале наблюдения под воздействием входных сигналов представляет соотношение вида

(t₀ × C) × (T × X) × C

Процесс переходов системы в фазовом пространстве, наблюдаемый во времени, представляет собой множество отношений упорядоченности декартово произведение, что видно из рисунка.

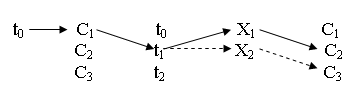
Математическая модель этого процесса имеет вид отображения

P: (t₀ × Z) × (t₁ × X) → Z_t1

В общем случае ее можно записать в следующем виде

Сt = P{(t₀, ..., t), C_t0, X},

где Р — множество операторов перехода системы в фазовом пространстве состояний.

Выходная реакция системы в любой момент времени определяется состоянием системы в этот момент времени. Поэтому справедливо следующее соотношение.

Y_t = G{Z_t}.

где C_Z — множество оператор выходов.

Таким образом, динамическая система представляет собой множество

S = (P, G, X, Y, C, T).

Как следует из соотношений ( и ) это множество можно представить в виде декомпозиции

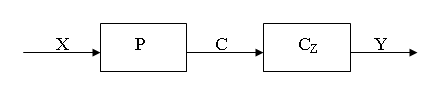
Наиболее общими свойствами динамических систем являются устойчивость и управляемость.

Устойчивость динамических систем

Пусть множество входных воздействий содержат элементы в интервале (-∞; +∞) и пусть p = [p_k, k={1,k}] семейство операторов перехода, которые при заданном множестве входных воздействий X^ реализуют полное множество Z^ состояний системы мощностно Z^ = M₁ ⋅ M₂ ⋅ ... ⋅ M_N

Реальный объект имеет вполне определенный оператор переходов p_k ⊂ p и находится под воздействием определенного множества входных сигналов X ⊂ X^. Если для заданных Х и p_k существует соотношение

Z_t = p_k{(t₀, t), Z_t0, X},

то множество [Z_t0, Z_t1, ..., Z_t] на любом интервале наблюдения является замкнутым, а система

S = [p_k, G, X, Y, T]

устойчивой относительно множества входных воздействий Х.

Управляемость динамических систем

В общем случае задача управления формируется в следующем виде. Известно множество входных сигналов Х, и семейство операторов перехода Р и выходов G. Задано необходимое значение выхода Y_t в момент времени t. Найти управляющее воздействие v ∈ V обеспечивающие выбор операторов перехода p ∈ P и выхода g ∈ G обеспечивающие необходимое y_t.

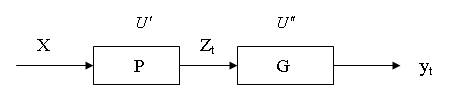
Исходя из общей формулировки задачи управления, необходимо различать управление множеством выходов. Достижение цели управления обеспечивается выбором операторов p и q.

Система является управляемой, если для заданных X_t ⊂ X и C_t ⊂ C, существуют такие C_t0 ⊂ C, что существуют p(C,X_t) ⊂ P или g(C_t,y_t).

Отсюда следует, что управление может осуществляться начальным состоянием, операторами переходов и выходов. При этом задача управления сводится к следующему. Известно x ⊂ X, p ⊂ P, g ⊂ G. Задано y_t = y ⊂ Y. Необходимо найти v ⊂ V при котором p(c_t = c ⊂ C, x_t = x ⊂ X) и g(y_t = y ⊂ Y, c_t = c ⊂ C).

Интегративные свойства систем

В предыдущих разделах были рассмотрены структурные и динамические свойства систем, которые не связаны с какой либо физической природой объекта анализа и вытекают из математических свойств абстрактных множеств.

Интегративные свойства систем охватывают структурные и динамические свойства одновременно, носят прикладной характер и базируются на принципах и закономерностях естествознания. Они проявляются на множестве отношений свойств объекта и внешней среды. Т.е. отражают результат их взаимодействий в виде изменений объекта и внешней среды.

Характер взаимодействия объекта и внешней среды может быть различным: сплоченным или разобщенным. При этом соответственно и результаты взаимодействия могут быть положительными и отрицательными. В этом смысле рассмотрим две группы наиболее общих интегративных свойств, связанных с оценкой возможности возникновения положительных результатов (качество и эффективность) и отрицательных результатов (безопасность и живучесть).

Качество системы

Качество системы представляет виртуальную оценку возможности получения положительного результата взаимодействия объекта с внешней средой.

Под качеством понимается обобщенная положительная характеристика системы, которая показывает ее полезность для макросистемы, состоящей из двух подсистем: объекта и внешней среды.

Для выражения качество служит показателем качества — положительное свойство системы. Суждение о качестве системы основывается на сравнении показателя качества одной системы с показателем качества другой системы реально существующей или виртуальной. Решение о качестве принимается на основе критерия — правило выбора альтернатив (вариантов).

Рассмотрим следующую задачу. Пусть А  — множество свойств виртуальной системы, т. е. потребностей макросистемы. В — множество свойств системы. Здесь возникают несколько вариантов, представленные на рисунках.

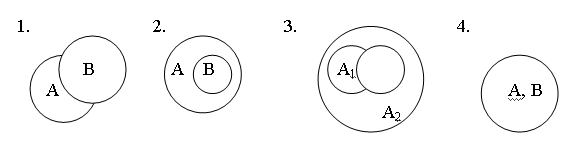
Рис. — Соотношение множеств свойств систем А и A₁ и потребностей макросистемы В.

1. Система не удовлетворяет потребностям макросистемы и следовательно непригодна.
2. Система удовлетворяет потребностям по возможности по использование ее ресурса нерационально |А| > |B|.
3. Система A₂ удовлетворяет потребностям макросистемы, поэтому она превосходит систему A₁.
4. Система пригодна и рационально расходует свой ресурс.

Из рассмотренных примеров вытекают три основных критерия качества системы пригодности, превосходства и оптимальности.

Эффективность

Понятие эффективность связано с целенаправленными процессами, т. е. процессом функционирования некоторой системы, которая организуется и проводится для достижения определенной цели, т. е. получение определенного результата.

Характеризуя целенаправленный процесс необходимо различать качества определенных получаемых результатов и качество множества результатов рассматриваемых как единое целое. Последнее характеризует уровень достижения цели. Это свойство будет называться эффективностью целенаправленного процесса (операции).

Свойство обобщенного результата операции условно можно разделить на три группы:

• результативность (целевой эффект)
• ресурсоемкость
• оперативность (расход времени)

Соответственно показатели эффективности отражают одну из групп свойств или совместно все. В этой связи эффективностью называют комплексное свойство целенаправленного процесса.

Показатели эффективности

Показатели эффективности должны удовлетворять ряду общих обязательных требований. Основными из них являются: представительность, полнота, стохастичность, простота.

Представительность означает, что эффективность должна оцениваться относительно главной цели операции, а показатель должен иметь прямое отображение цели, характеристик процесса и внешней среды.

Количественная величина показателя должна быть чувствительна к изменению характеристик процесса и случайных факторов во внешней среде. А математическая модель должна обеспечивать проведение необходимых измерений и вычислений в приемлемые сроки.

В общем виде показатель эффективности имеет вид вектора

α = <R_ц, R_р, T>

где R_ц — целевые эффекты,

R_р — ресурсоемкость, Т — затраты времени.

Поскольку процесс функционирования системы протекает во внешней среде с характеристиками V, состав этих характеристик оказывает влияние на R_ц, R_р и Т то реально величина Э представляет множество

Э(V) = [e(u_n), n={1,N}]

Поэтому цель операции формально можно представить в следующем виде.

Э(V) ⊂ {Э_дон.}.

↑	Оглавление
←	Лекция 6, «Информационное описание и моделирования систем»	Лекция 8, «Структура системного анализа»	→