«Системный анализ и проектирование»

Е. Н. Живицкая

↑	Оглавление
←	Лекция 10, «Энтропия и количество информации»	Лекция 12, «Языки описания выбора»	→

Лекция 11: О результатах теории информации

Теория информации приводит к ряду новых понятий, описывающих информационные процессы, происходящие в системах, к введению новых количественных параметров, позволяющих производить измерения и расчеты. Однако главная ценность теории информации состоит в полученных новых результатах, в открытии ранее неизвестных свойств систем. Чтобы познакомиться с основными из этих результатов, рассмотрим еще некоторые понятия и параметры информационных процессов и систем.

Избыточность

Одной из важнейших характеристик сигнала является содержащееся в нем количество информации. Однако по ряду причин количество информации, которое несет сигнал, обычно меньше чем то, которое он мог бы нести по своей физической природе. Информационная нагрузка на каждый элемент сигнала меньше той, которую элемент способен нести. Для описания этого свойства сигналов введено понятие избыточности и определена ее количественная мера.

Пусть сигнал длиной n символов содержит количество информации I. Если это представление информации обладает избыточностью, то такое же количество информации I может быть представлено с помощью меньшего числа символов. Обозначим через nо наименьшее число символов, необходимое для представления I без потерь. На каждый символ в первом случае приходится I₁ = I/n бит информации, во втором I₁^max = I/n₀ бит. Очевидно, I = n⋅I₁ = n₀⋅I₁^max. В качестве «меры избыточности» R принимается относительное удлинение сигнала, соответствующее данной избыточности:

R = (n - n0)/n = 1 - (n0/n) = 1 - (I1/I1max).

(1)

В дискретном случае имеются две причины избыточности: неравновероятность символов и наличие статистической связи между символами. В непрерывном случае — это неэкстремальность распределений (т.е. отклонение от распределений, обладающих максимальной энтропией.

Не следует думать, что избыточность — явление всегда отрицательное. При искажениях, выпадениях и вставках символов именно избыточность позволяет обнаружить и исправить ошибки.

Скорость передачи и пропускная способность

Следующим важнейшим понятием является скорость передачи информации. Так называется количество информации, передаваемое в единицу времени. Эта величина определяется по формуле

R = H(X) - H(X/Y),

(2)

где указанные энтропии исчисляются на единицу времени.

В дискретном случае единицей времени удобно считать время передачи одного символа. Тогда в (2) фигурирует априорная и апостериорная энтропии на один символ. Для непрерывных каналов единицей времени может служить либо обычная единица (например, секунда), либо интервал между отсчетами. Тогда в (2) вводят соответствующие дифференциальные энтропии. Для более наглядного представления о величине R укажем, что темп обычной речи соответствует скорости порядка 20 бит/с, муравьи обмениваются информацией путем касания усиками со скоростью около 0,1 бит/с.

Скорость передачи информации по каналу связи зависит от многих факторов — от энергии сигнала, числа символов в алфавите, избыточности, полосы частот, способа кодирования и декодирования. Если имеется возможность изменять некоторые из них, то, естественно, следует делать это так, чтобы максимально увеличить скорость. Оказывается, что существует предел, выше которого увеличение скорости невозможно. Этот предел называется «пропускной способностью канала»:

C = sup(RA),

(3)

где R_A — скорость передачи информации при условиях А, {A} — множество вариантов условий.

Так как множество {A} можно определить по разному, то имеет смысл говорить о нескольких типах пропускной способности. Наиболее важным является случай, когда мощность сигнала (объем алфавита) фиксирована, а варьировать можно только способ кодирования. Именно таким образом пропускную способность определил К.Шеннон.

Для представления о порядках величины С приведем примеры. Прямыми измерениями установлено, что пропускная способность зрительного, слухового и тактильного каналов связи человека имеют порядок 50 бит/с (вопреки распространенному мнению о сильном отличие зрительного канала). Возможно, ограничивающим фактором являются не сами рецепторы, а нервные волокна, передающие возбуждение. Если включить в канал и «исполнительные» органы человека (например, предложить ему нажимать кнопку в темпе получения сигналов), то пропускная способность близка к 10 бит/с. Интересно отметить, что многие бытовые технические устройства слабо согласованы с органами чувств человека. Например, канал телевидения имеет пропускную способность в десятки миллионов бит/с.

Кодирование в отсутствии шумов

С помощью введенных понятий можно рассмотреть многие информационные процессы. Начнем с дискретных систем без шумов. Здесь главное внимание привлекает проблема эффективности. Важно, чтобы данная информация заняла в запоминающем устройстве как можно меньше ячеек, при передаче желательно занимать канал связи на максимально короткий срок. В такой постановке задачи легко распознается проблема устранения всякой избыточности и эта проблема далеко не тривиальна.

Пусть алфавит системы состоит из m символов. Средствами этого алфавита требуется представить любой из М возможных сигналов {u_k}, k = 1...m, вероятности которых {p(u_k)} заданы. Обычно каждый из сигналов, подлежащих передаче, невозможно обозначить только одним символом и приходится ставить им в соответствие некоторые последовательности символов, которые называют «кодовыми словами». Так как возможна последовательная передачи разных кодовых слов, то они не только должны различаться для разных u_k, но и не должны быть продолжением других, более коротких. Пусть сигналу u_k cоответствует кодовое слово длиной l_k символов. При стационарной передаче сигналов с вероятностями {p(u_k)} средняя длина кодового слова равна cумме всех l_k⋅p(u_k). Возникает вопрос о том, как выбрать L и {l_k}. Вопрос не имеет смысла, пока не задан критерий выбора этих величин. Определим этот критерий так: L и {l_k} должны быть минимальными величинами, такими, при которых еще не происходит потери информации. Напомним, что в отсутствие шумов среднее количество информации на один элемент u_k ансамбля {u_k} равно энтропии этого ансамбля, т.е.

H(U) = -∑p(u_k)⋅log(p(u_k))

а индивилуальное количество информации есть

i(u_k) = -log(u_k).

С другой стороны, на один символ придется максимальное количество i информации, если символы равновероятны и независимы; при этом i = log(m). Поскольку кодирование должно вестись без потерь информации, сразу получаем

	[H(U)/log(m)] ≤ L,	(4)
	[i(uk)/log(m)] < lk ≤ [i(uk)/log(m)] + 1.	(5)

Так из общих соображений находим нижние границы для L и l_k. В теории информации доказываются теоремы об условиях достижимости этих границ. Мы не будем приводить эти теоремы. Укажем лишь, что речь идет не только о принципиальной возможности: разработаны процедуры построения кодов, обеспечивающих безизбыточное кодирование (либо сколь угодно близкое к нему).

Кодирование при наличие шумов

Наиболее интересные и важные результаты были получены при рассмотрении передачи информации по каналам связи с шумами. В этом случае безизбыточное кодирование приведет к безвозвратным потерям информации: искаженный символ нельзя ни обнаружить, ни исправить. Для борьбы с влиянием помех необходимо ввести избыточность в сигнал. Основываясь на интуитивных соображениях, легко прийти к выводу, что при неограниченном повышении требований к малости вероятности ошибки избыточность (при любом способе кодирования) должна неограниченно возрастать, а скорость передачи — стремиться к нулю. Здесь мы имеем яркий пример того, как интуиция может привести к сильному заблуждению. К.Шеннон показал, что «существуют такие способы введения избыточности, при которых обеспечиваются одновременно и сколь угодно малая вероятность ошибки и конечная (отличная от нуля) скорость передачи информации. Причем эта скорость может быть сколь угодно близкой к пропускной способности канала». Это замечательное открытие и привлекло столь большое внимание к теории информации. Воспроизведем упрощенное доказательство указанного утверждения.

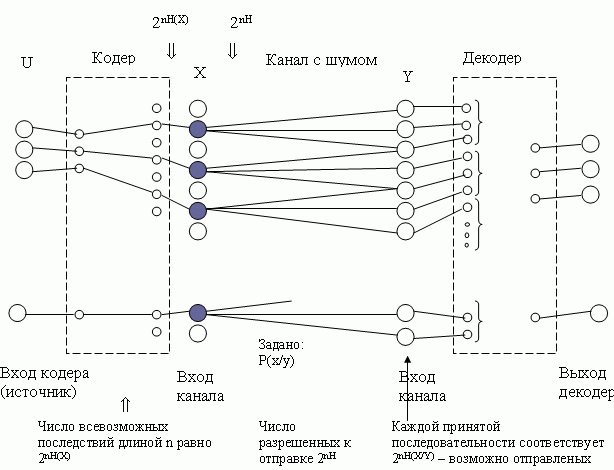
Рис.11.1 — Схема передачи по каналу с шумом

Будем считать, что на вход кодера сигналы поступают закодированными безизбыточно. Кодер вносит в сигнал избыточность, увеличивая длительность кодовых слов. Число возможных последовательностей сразу резко увеличивается. Но избыточность и состоит в том, что к отправке предназначаются не все из них, а лишь «разрешенные» (на рис. отмечены черными кружками). Согласно фундаментальному свойству энтропии, число всевозможных последовательностей длины n равно 2^n⋅H(X), а число разрешенных к отправке равно 2^n⋅H < 2^n⋅H(X) (считаем, что энтропия исчисляется в битах); Н — энтропия на символ во множестве разрешенных к отправке последовательностей (»энтропия источника», или «скорость создания информации»), H(X) — энтропия на символ во множестве всевозможных последовательностей. В результате воздействия шумов какие-то из символов отправленной последовательности подменяются другими и на приемный конец поступает другая, отличная от отправленной, последовательность. Поскольку p(x/y) считается известной, каждой принятой последовательности соответствует 2^n⋅H(X/Y) возможно отправленных. Декодирование, (т.е. принятие решения о том, какая последовательность была отправлена) можно выразить как разбиение всего множества Y принимаемых последовательностей на 2^n⋅H подмножеств, сопоставляемых с разрешенными к отправке. Если, например, принят сигнал i-й группы, то считается, что был послан i-й разрешенный сигнал, который и выдается в «чистом» виде получателю. Итак, в построенной модели проблема выбора кода (способа передачи) состоит в размещении разрешенных последовательностей среди множества всевозможных на передающем конце и в разбиении этого множества из 2^n⋅H(X) последовательностей на 2^n⋅H подмножеств на приемном конце.

Идея Шеннона состоит не в том, чтобы указать некоторый регулярный способ кодирования со сколь угодно малой вероятностью ошибки, а в том, чтобы показать, что такой код вообще существует.

Рассмотрим класс всевозможных кодов, которые получаются, если разрешенные последовательности размещать среди всевозможных случайным образом, а в качестве декодирующего подмножества брать 2^n⋅H(X/Y) последовательностей высоковероятной группы, соответствующей принятому сигналу. Вероятность ошибки при этом равна вероятности того, что среди 2^n⋅H(X/Y) последовательностей окажется более одной разрешенной. Так как код получается в результате случайного (равновероятного) выбора 2^n⋅H последовательностей среди 2^n⋅H(X), то вероятность того, что данная последовательность окажется разрешенной, равна

2n⋅H/2n⋅H(X) = 2n⋅(H-H(X)).

(6)

Средняя вероятность того, что в декодирующем подмножестве из 2^n⋅H(X/Y) последовательностей имеется только одна разрешенная, выразится соотношением

P = {1 - 2n⋅(H-H(X))}2n⋅H(X/Y) - 1.

(7)

Это и есть вероятность безошибочного приема. Поскольку

H < C = H(X) - H(X/Y),
H - H(X) = -H(X/Y) - ν, где ν > 0

Отсюда (пренебрегая единицей по сравнению с 2^n⋅H(X/Y) находим

P = {1 - 2^n⋅(H-H(X))}^{2n⋅H(X/Y) - 1}.

Логарифмируя и применяя правило Лопиталя, легко показать, предел Р = 1, при n стремящемся к бесконечости, т.е. при кодировании достаточно длинными блоками средняя вероятность ошибки может быть сделана сколь угодно малой. Доказательство завершается утверждением, что существуют коды с вероятностями ошибок меньше средней.

Пропускная способность гауссова канала связи

Перейдем теперь к знакомству с основными результатами для систем с непрерывными сигналами. Наиболее известным выводом теории является формула для пропускной способности гауссова канала связи.

Гауссовым каналом называется канал связи, для которого выполняются следующие условия:

1. сигналы и шумы в нем непрерывны;
2. канал занимает ограниченную полосу частот шириной F;
3. шум n(t) в канале распределен нормально (»гауссов шум»);
4. спектр мощности шума равномерен в полосе частот канала и равен N единиц мощности на единицу полосы частот;
5. средняя мощность полезного сигнала фиксирована и равна P₀;
6. сигнал и шум статистически независимы;
7. принимаемый сигнал y(t) есть сумма полезного сигнала и шума, т.е. y(t) = x(t) + n(t) — «шум аддитивен».

Эти предположения позволяют вычислить пропускную способность гауссова канала. Во-первых, ограниченность полосы частот позволяет применить теорему отсчетов и вести рассуждения для каждого отсчета в отдельности. Далее, аддитивность шума и его независимость от X позволяют представить количество информации в Y об Х в виде

I(X,Y) = h(Y) - h(Y/X) = h(Y) - h(X+N/X) = h(Y) - h(N),

(8)

где h(N) — дифференциальная энтропия шума. Следовательно, пропускная способность такова:

C = max(h(y)-h(N))

Согласно условиям 3) и 4), имеем

h(N) = F⋅log(2⋅π&sdote⋅N⋅F).

(9)

В силу условий 4)-7) мощность принимаемого сигнала есть

M(Y2) = P0 + n⋅F.

(10)

Максимум h(Y) при условии (10) достигается в случае нормального распределения, т.е.

max(h(y)) = F⋅log[2⋅πe(P0) + N⋅F]

(11)

Так как шум имеет равномерный спектр (условие 4) и спектр смеси y(t) также равномерен (вследствие независимости отсчетов), то и полезный сигнал должен иметь равномерный спектр. Вводя спектральную плотность P = P₀/F и вычитая равенство (9) из (11), получаем известную формулу Шеннона-Таллера

C = F⋅log(1 + P/N).

Таким образом, мы не только определили пропускную способность, но и заодно показали, что она реализуется, если полезный сигнал закодировать так, чтобы его спектр был равномерным в представленной полосе частот, а распределение мгновенных значений — нормальным.

Дальнейшие обобщения связаны с рассмотрением «небелых» сигналов и шумов (предполагается зависимость от частоты их спектральных мощностей P(f) и N(f), а также с допущением случайности величины P (например, в случае замирания радиосигналов). Решение возникающих при этом задач можно найти в литературе по теории информации.

Подведем итог

Теоремы Шеннона о кодировании в каналах без шумов и при наличии шумов, приведенные в данном параграфе относятся к числу основных результатов теории информации. Практически самым важным открытием в теории информации является установленная Шенноном возможность практически безошибочной передачи информации по каналу с шумом со скоростью, близкой к пропускной способности.

Заключение

Отметим, что наиболее важные результаты тории информации — теоремы о кодировании — являются теоремами о существовании и носят асимптотический характер, т.е. не являются конструктивными. Однако уже само знание потенциальных возможностей имеет огромное значение: сравнение характеристик реальных систем с теоретическими пределами позволяет судить о достигнутом уровне и о целесообразности затрат на его повышение. Прикладные же вопросы рассматриваются в специальном разделе теории информации — теории кодирования, которая изучает способы построения конкретных кодов и их свойства.

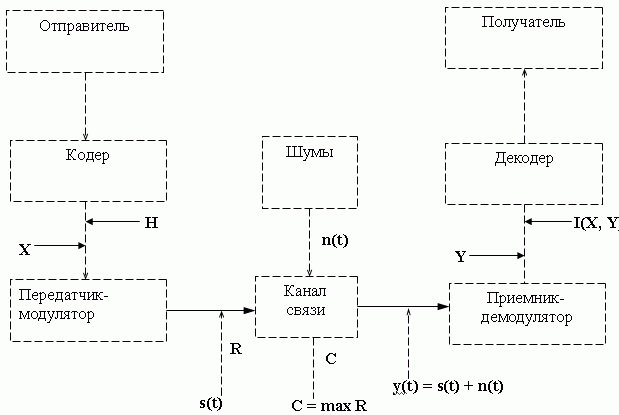
Для напоминания об основных понятиях теории информации приведем вариант блок-схемы системы передачи информации. На этом рисунке приведено большинство введенных в данной главе понятий и обозначений.

Знание теории информации выходит далеко за рамки теории связи. Именно ее появление привело к более глубокому пониманию открытых ранее закономерностей природы, например, второго закона термодинамики. Вместе с тем некоторые специалисты различных отраслей науки некритически распространяли методы и конкретные результаты теории информации на любые информационные процессы в реальном мире. Уже сам Шеннон заметил эту тенденцию и настоятельно предостерегал от того, чтобы ее безоглядно следовать. Дело в том, что шенноновское количество информации является характеристикой, лишь с одной стороны описывающей информационные отношения. Именно эта сторона — соответствие состояний — играет главную роль в технических устройствах. Однако в этом соответствии не проявляют себя такие свойства информации, как смысл, доброкачественность (степень истинности), ценность, полезность, временное старение, причинно-следственная направленность и т.д. —  свойства, весьма существенные для информационных отношений с участием живых организмов, людей, коллективов. К развитию новых подходов в теории информации толкает сильное «внешнее» давление общественной практики. Масштабы и значение информационных потоков в современном обществе так резко возросли в последние годы, что даже возникло образное выражение «информационный взрыв». Появилась новая отрасль — «индустрия обработки данных», затраты на которую в промышленно развитых странах превосходят затраты на энергетику. Этой общественной потребности отвечает и возникновение новой отрасли науки — информатики.

Системный анализ неизбежно выходит на исследование ресурсов (наличных и необходимых), которые потребуются для решения анализируемой проблемы. При этом информационные ресурсы играют первостепенную роль наряду с ресурсами материальными, энергетическими, временными, кадровыми.

↑	Оглавление
←	Лекция 10, «Энтропия и количество информации»	Лекция 12, «Языки описания выбора»	→