«Системный анализ и проектирование»
Е. Н. Живицкая
| ↑ | Оглавление | ||
| ← | Лекция 13, «Выбор в условиях статической неопределенности» | Лекция 15, «Декомпозиция систем» | → |
Лекция 14: Групповой выбор
В человеческом обществе единоличное принятие решений является не единственной формой выбора. «Ум — хорошо, а два — лучше», гласит поговорка, имеющая в виду тот случай, когда оба ума с одинаковыми намерениями пытаются найти хороший выбор. Этот случай мы и рассмотрим в данном параграфе.
Описание группового выбора
Итак, пусть на множестве альтернатив Х задано n в общем случае различных индивидуальных предпочтений. Для определенности будем говорить о бинарных отношениях R 41 0,R 42 0,...,R 4n 0
Ставится задача о выработке такого нового отношения R , которое согласует индивидуальные выборы, выражает в каком-то смысле «общее мнение» и принимается за групповой выбор. Очевидно, что это соотношение должно быть какой-то функцией индивидуальных выборов: R = F(R 41 0,R 42 0,...R 4n 0).
Различным функциям согласования будут отвечать разные функции F. В принципе, т.е. теоретически функции F могут быть совершенно произвольными, но главный вопрос состоит в том, чтобы правильно отобразить в функции F особенности конкретного варианта реального группового выбора.
Различные правила голосования. Одним из наиболее распространенных принципов согласования — правило большинства: принятой всеми считается альтернатива, получившая наибольшее число голосов. Правило большинства привлекательно своей простотой и демократичностью, но имеет особенности, требующие осторожного обращения с ним.
Прежде всего, оно лишь обобщает индивидуальные предпочтения, и его результат не является критерием истины. Только дальнейшая практика показывает, правильным или ошибочным было решение, принятое большинством голосов. Само голосование — лишь форма согласования дальнейших действий. (Этот вопрос, однако, формально находится вне нашего рассмотрения: ведь мы обсуждаем выбор в условиях определенности, а здесь речь зашла о выборе определенной альтернативы с неопределенными последствиями).
Во-вторых, даже в простейшем случае выбора одной из двух альтернатив легко представить себе ситуацию, когда правило большинства не срабатывает, например, разделение голосов поровну при четном числе голосующих. Это порождает варианты: «председатель имеет два голоса», «большинство простое (51%)», «подавляющее большинство (около 3/4)», «абсолютное большинство (близкое к 100%)», наконец, «принцип единогласия (консенсус, право вето)».
Подчеркнем, что при любом из этих вариантов подразумевается отказ от принятия решения, если ни одна из альтернатив не получила необходимого процента голосов. Поскольку в реальной жизни отказ от дальнейших действий, следующих за решением, бывает недопустим, то разрабатываются различные приемы, сокращающие число ситуаций, приводящих к отказу.
Парадоксы голосования
Следующая особенность правила голосования — это возможность отказа от выбора из-за не достижения требуемого большинства. Казалось бы, исключив такую возможность можно обеспечить принятие решения в любых случаях. Однако здесь мы приходим еще к одной особенности правила голосования — его нетранзитивности.
Пример
Каждая из трех группировок законодателей, образующих большинство лишь попарно, выдвинули свой вариант законопроекта: a, b, и c. Чтобы гарантировать большинство на каждом шаге процедуры, альтернативы предъявляются попарно. Каждая сторона руководствуется при этом своим набором предпочтений; пусть это соответственно последовательности (a > b > c), (b > c > a) и (c > a > b).
После голосования по паре (a,b) в результате получаем два голоса против одного: a > b; по паре (b,c) имеем b > c; по паре (c,a) имеем c > a. Видим, что голосование большинством не привело к выяснению порядка альтернатив: a > b > c > a.
Если же применить процедуру, при которой после рассмотрения очередной пары отвергаемая альтернатива заменяется новой, окончательно принятое решение будет зависеть от порядка предъявления альтернатив. При порядке (a, b, c) выбирается с; при порядке (b, c, a) выбор остановится на а; при порядке (a, c, b) — на b. Очевидно, что если таким образом будет приниматься законопроект, голосование будет выражать не мнение большинства, а мнение организатора голосования.
Здесь мы рассмотрели лишь частный пример более общего явления, получившего название — парадокса Эрроу.
Пример
Вмешательство коалиций в механизм голосования. Рассмотрим еще одну особенность голосования, которую следует иметь в виду на практике. При многоступенчатом голосовании по правилу большинства коалиция, находящаяся в меньшинстве, может добиться принятия своего решения. На рисунке изображено голосование по три большинством в 2/3 на каждой ступени.
Видно, что уже на второй ступени меньшинство может навязать свое мнение большинству. Если число ступеней не ограничивать, то теоретически побеждающее таким образом меньшинство может быть сколь угодно малым.
Подведем итог
Широко применяемая и во многих случаях успешная процедура голосования наряду с очевидными достоинствами обладает рядом скрытых особенностей, которые могут ослабить и даже извратить демократический характер. Знание таких «парадоксов» голосования необходимо для специалистов по системам.
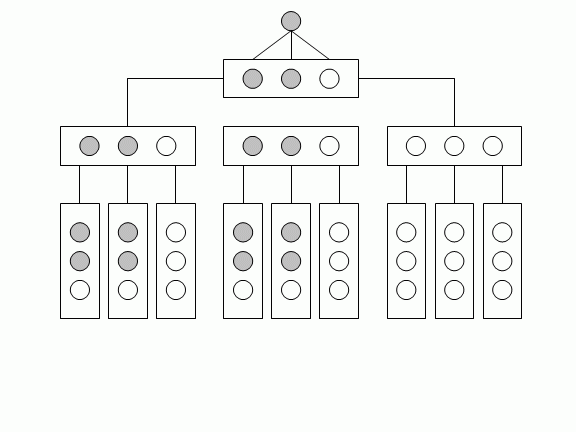
Рис.14.1
| ↑ | Оглавление | ||
| ← | Лекция 13, «Выбор в условиях статической неопределенности» | Лекция 15, «Декомпозиция систем» | → |