«Системный анализ и проектирование»
Е. Н. Живицкая
| ↑ | Оглавление | ||
| ← | Лекция 21, «Современные тенденции в области системного анализа» | Лабораторная работа 1, «Разработка функциональной модели для решаемой задачи» | → |
Лекция 22: Решение хорошо структуризованных проблем
Для решения проблем этого класса широко используются математические методы И.О. В операционном исследовании можно выделить основные этапы:
- Определение конкурирующих стратегий достижения цели.
- Построение математической модели операции.
- Оценка эффективностей конкурирующих стратегий.
- Выбор оптимальной стратегии достижения целей. Математическая модель операции представляет собой функционал E = f(x∈x^, {α}, {β})⇒ extz
Е — критерий эффективности операций;
x — стратегия оперирующей стороны;
a — множество условий проведения операций;
b — множество условий внешней среды.
Модель позволяет оценить эффективность конкурирующих стратегий и выбрать из их числа оптимальную стратегию.
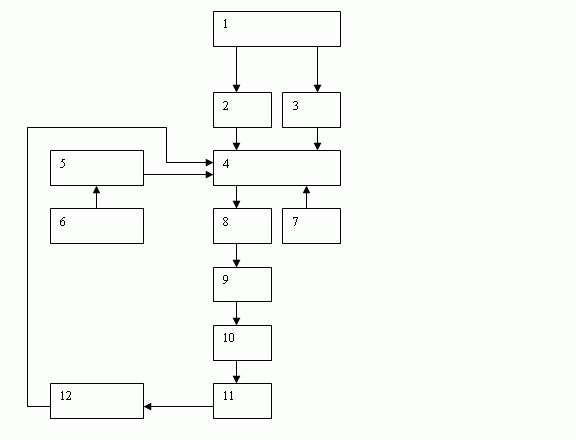
Рис. 22.1 — Выбор оптимальной стратегии достижения целей
- постоянство проблемы
- ограничения
- критерий эффективности операций
- математическая модель операции
- параметры модели, но часть параметров, как правило, не известна, поэтому (6)
- прогнозирование информации (т.е. нужно предугадать ряд параметров)
- конкурирующие стратегии
- анализ и стратегии
- оптимальная стратегия
- утвержденная стратегия (более простая, но которая удовлетворяет еще ряду критериев)
- реализация решения
- корректировка модели
Критерий эффективности операции должен удовлетворять ряду требований:
- Представительность, т.е. критерий должен отражать основную, а не второстепенную цель операции.
- Критичность — т.е. критерий должен изменяться при изменении параметров операций.
- Единственность, так как только в этом случае возможно найти строгое математическое решение задачи оптимизации.
- Учет стохастичности, которая связана обычно со случайным характером некоторых параметров операций.
- Учет неопределенностей, которая связана с отсутствием какой-либо информации о некоторых параметров операций.
- Учет противодействия, которое вызывает часто сознательный противник, управляющий полными параметрами операций.
- Простая, т.к. простой критерий позволяет упростить математические выкладки при поиске opt. решения.
Приведем схему, которая иллюстрирует основные требования к критерию эффективности исследования операций.
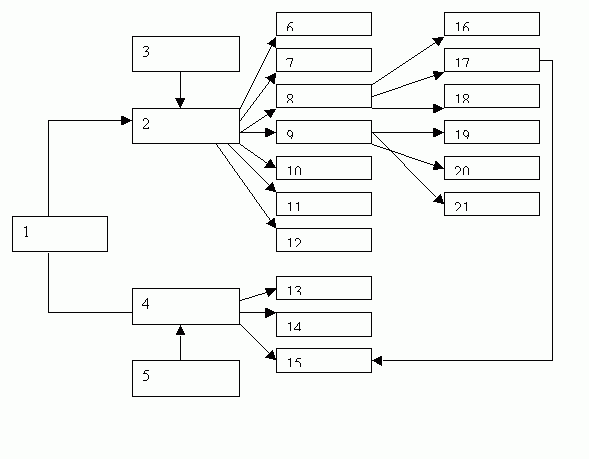
Рис. 22.2 — Требования к критерию эффективности исследования операций
- постановка проблемы (вытекают 2 и 4 (ограничения));
- критерий эффективности;
- задачи верхнего уровня
- ограничения (мы организуем вложенность моделей);
- связь с моделями верхнего уровня;
- представительность;
- критичность;
- единственность;
- учет стохастичности;
- учет неопределенности;
- учет противодействия (теория игр);
- простота;
- обязательные ограничения;
- дополнительные ограничения;
- искусственные ограничения;
- выбор главного критерия;
- перевод ограничений;
- построение обобщенного критерия;
- оценка математического отид-я;
- построение доверительных интервалов:
- анализ возможных вариантов (есть система; мы точно не знаем, какова интенсивность вх. потока; мы можем только с определенной вероятностью предположить ту или иную интенсивность; затем взвешиваем выходящие варианты ).
Единственность — чтобы можно было решить задачу строго математическими методами.
Пункты 16, 17 и 18 — это способы, которые позволяют избавиться от многокритериальности.
Учет стохастичности — большая часть параметров имеет стохастическое значение. В ряде случаев стох. мы задаем в виде ф-и распределения, следовательно, сам критерий необходимо усреднить, т.е. применять математические ожидания, следовательно, п.19, 20, 21.
| ↑ | Оглавление | ||
| ← | Лекция 21, «Современные тенденции в области системного анализа» | Лабораторная работа 1, «Разработка функциональной модели для решаемой задачи» | → |