«Системный анализ и проектирование»
Е. Н. Живицкая
| ↑ | Оглавление | ||
| ← | Лекция 4, «Математическое описание систем» (1 часть) | Лекция 6, «Основные системно-теоретические задачи» | → |
Лекция 5: Математическое описание систем (2 часть)
Энтропия и потенциальная функция При изучении систем с информационно-теоретической точки зрения часто ее описание дается на языке энтропии и потенциальных функций. По аналогии с классической механикой и теорией поля можно рассматривать реакцию системы на внешнее воздействие как динамическое изменение состояния системы, в процессе которого она стремится минимизировать некоторую потенциальную функцию. В зависимости от конкретного вида системы и принятых допущений такая динамика может быть локальной в смысле движения системы к относительному минимуму, ближайшему к текущему состоянию, или глобальной в смысле движения к абсолютному (глобальному) минимуму соответствующей потенциальной функции.
Приближенное описание динамического процесса на языке потенциальных функций включает следующие составляющие:
- пространство состояний (фазовое пространство) Z;
- набор входных функций X;
- гладкое отображение f: Z*X → R;
где R — есть пространство действительных чисел.
При этом предполагается, что система ведет себя так, что при фиксированном входе x ее н аблюдаемое состояние соответствует локальному либо глобальному минимуму потенциальной функции.
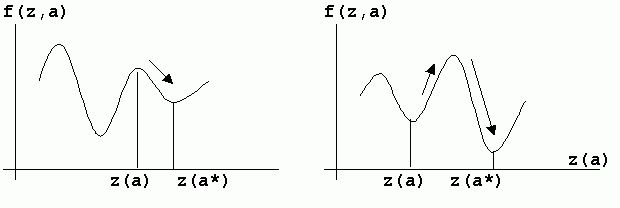
Рис.5.1 — Потенциальная функция системы
А) — движение к локальному минимуму;
В) — движение к глобальному минимуму;
f(z,a) — потенциальная функция;
z(a) — начальное положение системы, где а — внешний параметр.
Замена параметра а на а* приводит к изменению положения минимума функции f(z,a).
Использование потенциальной функции для описания хорошо изученных физических систем оказалось весьма удачной альтернативой внутренних описаний. Успешное применение такого подхода в классической физике обусловлено существованием незыблемых вариационных принципов, таких как принципы Гамильтона, Ферма и Даламбера. В большинстве случаев внутреннее описание физического процесса на языке потенциальных функций естественным образом вытекает из описания с пoмощью потенциальных функций в силу уравнений Гамильтона-Якоби и Эйлера-Лагранжа.
В системах, которые являются предметом изучения общественных наук, возможность использования такого описания не столь обоснована из-за сложности применения вариационных принципов. Однако в ряде случаев при анализе устойчивости или в теории катастроф знание точного вида потенциальной функции не является необходимым для определения важных качественных свойств системы — важен лишь сам факт ее существования.
С описанием системы на языке потенциальных функций тесно связана идея описания поведения систем с помощью энтропии. Как известно из классической термодинамики, энтропия является мерой беспорядка, существующего в данной физической системе. Мерой упорядоченности системы является отрицательная энтропия или негэнтропия. В основе описания динамического процесса с помощью энтропии лежит предположение преобразовании негэнтропии входа в информацию. Это означает, что все замкнутые системы изменяются таким образом, что минимизируют изменение энтропии. Таким образом, становится очевидной связь между описанием на языке потенциальных функций и энтропии.
Чтобы показать общность описаний в терминах энтропии, перечислим основные аксиомы релятивистской теории информации, развитой Джюмэри для динамических процессов.
Аксиома 1. Система является частью некоторой вселенной и развивается только постольку, поскольку она преследует некоторую цель.
Аксиома 2. Для достижения цели система воспринимает информацию I из окружающей среды и использует эту информацию для перестройки собственной организации (внутренней структуры) A, в результате которой увеличилась бы негэнтропия n, и для оказания воздействия L на окружающую среду.
Аксиома 3. (Принцип эволюции). Структурная энтропия Е системы определяется соотношением dE = dI/n и является неубывающей функцией эволюции.
Аксиома 4. Вселенная не может наблюдать собственную эволюцию. В силу этих аксиом уравнение состояния системы имеет вид:
f(He, Hi, ν) = 0, где
- He — внешняя энтропия системы по отношению к фиксированному наблюдателю R,
- Hi — внутренняя энтропия системы по отношению к наблюдателю R,
- ν — цель системы с точки зрения наблюдателя R.
При таком подходе к описанию системы наблюдатель (или лицо, принимающее решение) играет особую роль, причем особый упор делается на кинематический подход, основанный на аналогах преобразования Лоренца для двух наблюдателей R и R*.
Анализируя уравнение состояния, можно заметить, что знание функции f позволяет вычислить структурную энтропию Е c помощью соотношения, описывающего обмен информацией:
dI = α⋅dHe + β⋅dHi
Пример 1. Одномерная динамика
Рассмотрим простую динамическую систему x(t) = u(t),
где x(t) и u(t) — скалярные функции. Поскольку внешняя энтропия He обладает теми же свойствами, что и время t, произведем замену: t He. Более того, имеет смысл отождествить внутреннее состояние x с внутренней энтропией Hi. Тогда динамика системы эквивалентным образом описывается уравнением
dHi - u(He)⋅dHe = 0
Попытаемся теперь построить функцию состояния f в соответствии с приведенным выше ее определением. Из равнения состояния следует, что
df/dHe⋅dHe + df/dHi⋅dHi + df/dν⋅dν = 0
Не имея дополнительной информации о системе, можно предположить, что ее цель не меняется.Интегрируя уравнение динамики, получаем
f(Hi, He, ν) = H - ∫u(s)ds = 0
где He0 — внешняя энтропия в начальный момент времени t0.
Проведенный анализ показывает, что система x = u не определена с точки зрения обмена информацией с окружающей средой. Более того, такой обмен вообще не имеет места.
Пример 2. Стационарная динамика
Рассмотрим систему, описываемую уравнением
x(t) = Ψ[X(t)]
которое способом, аналогичным рассмотренному в примере А, можно привести к виду
dHi - Ψ(Hi)dHe = 0
Чтобы получить уравнение состояния, следует записать
df/dHi = 1 ⇒ f = Hi + k(He)
df/dHe = Ψ(Hi) ⇒ Ψ(Hi) = f(He)
Однако эти уравнения противоречивы и уравнение динамики следует рассматривать не как уравнение состояния, а как уравнение обмена информацией
dI = dHi - Ψ(Hi)dHe = 0
Следовательно, система не обменивается информацией с окружающей средой и развивается с постоянной структурной энтропией, что находится в соответствии с автономным характером системы.
В целом можно сказать, что «энтропийный» подход к анализу систем основан на трактовке системы, как некоторого единого целого. Отсюда следует, что понять сущность системы можно, лишь изучая ее взаимодействие с окружающей средой, т.е. с некой «вселенной». Взгляд на систему как на единое целое можно развить, введя понятие «связь». Весь комплекс связей и их характеристик приводит к понятию «структура» и «сложность» системы.
Множества и отношения
Рассмотрим теперь тип описания систем, который оказывается особенно эффективным при таких структурных исследованиях. Принято считать, что математическими абстракциями в основном оперирует теория множеств и отношений между их элементами. Поэтому целесообразно попытаться определить понятие системы в терминах этой теории. От конструктивного определения, естественно, можно потребовать, чтобы элементы соответствующих множеств и связывающие их отношения определялись спецификой конкретной системы. Тем не менее, если мы построим даже такое «специализированное» описание системы, оно даст весьма широкие возможности для анализа не только структуры системы, но и ее поведения в динамике.
В общем случае можно предположить, что существуют два конечных множества X и Y, элементы которых как-то связаны с системой. Это могут быть множества хищников и их жертв, множества типов автомобилей и дорог или множества предприятий службы быта и предлагаемых услуг. Для описания связи, существующей между двумя элементами (x,y) введем на прямом произведении X и Y бинарное отношение
λ, λ ∈ X×Y
Рассмотрим тривиальный пример, в котором X есть множество товаров, а Y — множество предприятий службы быта. Пусть для определенности
X = {x1(хлеб), x2(молоко), x3(марки), x4(обувь)}
Y = {y1(гастроном), y2(универмаг), y3(банк), y4(почта)}
Определим отношение A на прямом произведении X Y следующим образом:
Отношение A существует между xi и yj тогда и только тогда, когда xi можно купить в yj. В этом случае
λ = {(x1,y1), (x2,y1), (x3,y4), (x4,y2)}
Отношение A удобно представить матрицей инциденций:
| λ | y1 | y2 | y3 | y4 |
|---|---|---|---|---|
| x1 | 1 | 0 | 0 | 0 |
| x2 | 1 | 0 | 0 | 0 |
| x3 | 0 | 0 | 0 | 1 |
| x4 | 0 | 1 | 0 | 0 |
[Λ]ij = 1, (xi, yj) ∈ λ
С геометрической точки зрения отношение A определяет симплициальный комплекс KX(Y;A), в котором элементы множества Y рассматриваются как вершины, а элементы множества X являются симплексами. Так элемент x1(хлеб) является 0-симплесом, состоящим из вершины y1(гастроном). Если К не содержит r-симплексов (r ≥ 3), его можно изобразить на плоскости.Для предыдущего примера множество К имеет вид y1 y2 y4...
Хотя такая геометрическая структура не представляет особого интереса, тем не менее она все же показывает, что комплекс не содержит связных компонент и что вершина y3(банк) не играет никакой роли в анализе КX(Y;A).
Определив подходящие множества X и Y и отношение A, можно перейти еще к одному отношению. Это так называемое сопряженное отношение A*, которое получается, если поменять местами множества X и Y, и строится в соответствии с правилом: отношение A* существует между yi и xj тогда и только тогда, когда между xj и yi существует отношение A.
Матрица инциденций для A* получается транспонированием матрицы инциденций для A, т.е. A* = A×1. В результате получим геометрический комплекс КY(X;A*), в котором Х — множество вершин, а Y — множество симплексов. Тогда для рассмотренного выше примера комплекс имеет вид
![]()
который конечно же более содержателен, чем полностью несвязная структура КX(Y;): вершины x1(хлеб) и x2(молоко) связаны 1-симплексом (гастроном).
Продемонстрируем общность описания систем на языке множеств и бинарных отношений еще на одном примере.
Пример
Шахматы. Чемпион мира по шахматам Эммануил Ласкер как то заметил: «Если из 64 клеток шахматной доски вы контролируете 33, то преимущество на вашей стороне». Для нас данное высказывание представляет особый интерес, так как оно свидетельствует о том, что главное для шахматиста — это «стратегическое» содержание игры, которое мы можем выразить непосредственно в виде отношения между множеством фигур и множеством клеток шахматной доски.
Рассмотрим два отношения Aw и Ab, где Aw определяет связь между белыми фигурами и клетками доски, а Ab- та же связь для черных фигур.
Определим множества X и Y как
X = { фигуры }
X = { QR, QN, QB, Q, K, KB, KN, KR, QRP, QNP, QBP, QP, KP, KBP, KNP, KRP},
Y = { клетки }.
Мы здесь использовали стандартные международные обозначения для фигур: король — К, ферзь — Q, слон — В, конь — N, ладья — R, пешка — Р. При этом предполагается, что клетки доски также упорядочены соответствующим образом. Имеются в виду также следующие обозначения: буква Q в двухбуквенных символах означает ферзевый фланг, а К — королевский. Средняя буква в трехбуквенных символах (для пешек) обозначает фигуру, перед которой стоит данная пешка в начальной позиции.
Пусть заданы xi и yj; определим отношение Aw следующим образом:
(xi, yj) ∈ λw
тогда и только тогда, когда фигура xi атакует клетку yj. Под термином «атакует» понимается одна из следующих ситуаций:
- Если ход белых и если фигура xi не пешка и не король, то ход xi yj — правильный (разрешенный) ход.
- Если фигура xi пешка, то клетка yi находится под боем со стороны фигуры xi
- Если клетка yj занята белой фигурой, то фигура xi защищает эту фигуру.
- Если фигура xi — белый король, то клетка yj является соседней клеткой по отношению к клетке, занимаемой фигурой xi.
- Если клетка yj занята черной фигурой (но не королем) и если ход белых, то взятие данной черной фигуры фигурой xi — правильный ход.
- Черный король занимает клетку yj и находится под шахом фигуры xi.
Аналогично определяется отношение Ab.
Отметим, что Aw зависит от состояния игры (от расположения фигур на доске и от того, чей ход).
На этом рассмотрения настоящего примера заканчивается. Слушателю предоставляется возможность самостоятельно построить матрицы инциденций Aw и Ab.
Внимательный слушатель, несомненно, заметил некоторое сходство между теоретико-множественным описанием системы и более привычным описанием в терминах теории графов на языке узлов и дуг (или вершин и ребер). По существу, данное выше определение совпадает с описанием на языке теории графов, если определить X, Y как множества вершин, соединенных ребрами в соответствии с отношением A. Хотя при таком переходе в значительной степени утрачивается его гибкость, так при этом исчезает (в лучшем случае затушевывается) универсальность отношения A, тем не менее оно оказывается полезным во многих ситуациях.
Для теории систем наиболее существенным является описание динамики систем. Поэтому, чтобы понять, каким образом динамические переходы учитываются при теоретико-множественном описании процесса (системы) введем понятие образ. Вообще говоря, образ П есть отображение, которое каждому симплексу из комплекса ставит в соответствие определенное число, т.е.
П: σi → k
где К-определенная система чисел(действительных,целых и т.д.)
Поскольку каждый симплекс из К обладает некоторой геометрической размерностью, которая определяется числом его вершин, то образ П является ранжированным образом
П = П0⊕П1⊕...⊕ПN
где N = dim K — размерность наибольшего симплекса из К. Здесь каждое Пi является отображением, определенным только на множестве i-мерных симплексов из К.
Поясним понятие образа на примере «хищник-жертва». Напомним, что мы ввели два множества X — множество жертв и Y — множество хищников с матрицей инциденций:
| λ | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 |
|---|---|---|---|---|---|---|---|---|
| y1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| y2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| y3 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| y4 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| y5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| y6 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Таким образом, y1(люди) — это 3-симплекс, y4(птицы) -3-симплекс и т.д. Образ П при этом ставит в соответствие каждому симплексу некоторое число, скажем численность популяции в данный момент. Поскольку симплексы ранжированы по их размерности, то и Пi также ранжированы,
поэтому в каждый момент:
П0: {y5(рыбы)} — численность рыб, {y2(львы)} — численность львов
П1: {y3(слоны)} — численность слонов, {y6(лошади)} — численность лошадей
П2: — пусто
П3: {y1(люди)} — численность народонаселения, {y4(птицы)} — численность птиц
Полный образ для данной экосистемы имеет вид
П = П0⊕П1⊕П3
Динамику системы можно теперь описать изменениями образа П в каждый момент времени.
| ↑ | Оглавление | ||
| ← | Лекция 4, «Математическое описание систем» (1 часть) | Лекция 6, «Основные системно-теоретические задачи» | → |