«Системный анализ и проектирование»

Е. Н. Живицкая

↑	Оглавление
←	Лекция 5, «Математическое описание систем» (2 часть)	Лекция 7, «Основные положения теории систем» (1 часть)	→

Лекция 6: Основные системно-теоретические задачи

В предыдущем разделе мы рассмотрели некоторые основные способы описания динамики систем и их взаимодействия с человеком и окружающей средой. Вообще говоря, математическое описание позволяет выделить важные свойства рассматриваемой системы и формально определить взаимосвязи между ее различными компонентами. Поскольку использование тех или иных математических абстракций, которыми оперирует теория систем, зависит от поставленной задачи, то мы рассмотрим различные вопросы, такие как стохастические процессы, управляемые динамические системы (процессы), идентификация и т.д. Их изучение по-прежнему дает важные системно-теоретические результаты и на них в определенной степени, базируется изложение многих основных проблем теории больших систем.

Управляемы и неуправляемые динамические системы

Первые шаги, положившие начало развитию системного анализа, были сделаны античными астрономами. Не обладая средствами, с помощью которых можно было бы влиять на динамику изучаемых систем, они были вынуждены ограничить свой анализ лишь наблюдением, классификацией и возможно синтезом. Другими словами, их роль была пассивной: наблюдать. В аналогичном положении находятся современные исследователи, работающие, например, в области астрофизики. Они пока еще также вынуждены ограничиться только наблюдениями каких-то процессов, не имея возможности ими управлять.

В то же время, современный исследователь призван играть активную роль в развитии наблюдаемого процесса, поскольку именно он генерирует соответствующие внешние воздействия, гарантирующие удовлетворительное поведение системы. Разумеется, при таком подходе активного вмешательства возникает множество проблем психологического и морального характера. Подобное разделение на активную и пассивную или управляемую и неуправляемую динамику позволяет наиболее наглядно выявить отличие классического и современного взглядов на системный анализ.

«Кибернетический» или управленческий подход неизбежно приводит к изменению входов системы в зависимости от наблюдаемых ее выходов. При этом преследуется цель превратить некоторую первоначально независимую переменную в частично зависимую так, чтобы поведение системы в определенном смысле приближалось к некоторой стандартной (или желаемой) траектории. Такой процесс может оказаться более сложным, если имеется еще и обратное преобразование. Подобная ситуация типична для имитационного моделирования развивающихся систем. Обратное преобразование заключается в изменении и перестройке поведения системы по измеряемому выходу и является основой кибернетического регулирования и управления.

Идентификация

Начальный этап построения математической модели данной системы состоит в идентификации существенных переменных и их взаимосвязей. В зависимости от конкретного типа выбранного математического описания идентификация может включать: определение размерности пространства состояний, описание внутренней динамики системы и содержательных связей между множествами объектов, распределение вероятностей для случайных воздействий. Поскольку идентификация зависит от типа математического описания, которое в свою очередь зависит от того, насколько удачно проведена идентификация, то процесс построения модели является итерационным; сначала выбирают математическое описание, которое затем модифицируют в зависимости от результатов идентификации, что приводит к новому описанию, и процесс повторяют.

Наиболее глубоко разработанной проблемой идентификации систем является задача построения внутреннего описания линейного отображения вход-выход с постоянными коэффициентами. Для простоты изложения предположим, что данная система развивается в дискретном времени с начальным состоянием x₀=0 соответствующим начальному моменту времени t₀=0. Можно показать, что вход u(t) и выход y(t) системы связаны следующим соотношением

y(t) = ∑A_1-τ⋅u(τ)

где все матрицы {A_i} имеют размер p×m. Тогда описание типа «вход-выход» системы определяется последовательностью матриц {A₁,A₂, ...}. Если внутреннее описание системы, заданное соотношениями

x(t+1) = F[x(t)] + G[u(t)],
y(t) = H[x(t)],

согласуется с приведенным выше внешним описанием, то связь между матрицами F, G, H и {A_j} имеет вид:

At = H⋅Ft-1⋅G, t = 0, 1, 2, ...

{6.1}

Задача реализации для линейных динамических систем состоит в отыскании n×n, n×m, p×m матриц F, G и H соответственно, удовлетворяющих соотношению {6.1} и таких, что размерность внутреннего пространства состояний n минимальна. Иными словами, задача состоит в построении по возможности более компактной модели, согласующейся с наблюдаемыми данными.

Существуют «хорошие» алгоритмы решения задачи реализации, если справедливо следующие предложение: последовательность {A_i} обладает конечномерной реализацией. Для нелинейных отображений «вход-выход» общего вида подобных отработанных алгоритмов не существует, несмотря на попытки решения отдельных классов задач с некоторой линейной или алгебраической структурой.

В отличие от наиболее общих задач идентификации (типа от внешнего описания к внутреннему), так называемые задачи идентификации параметров исследовались более интенсивно. Эти задачи обычно возникают, когда имеется твердая уверенность в правильности определения основной внутренней структуры системы и невыясненными остаются только численные значения некоторых параметров.

Предположим, что динамика системы описывается дифференциальным (или разностным) уравнением:

dx/dt = f(x, u, a),
y(t) = h(x, a),

где а — вектор неизвестных параметров, которые следует определить, основываясь на значении наблюдаемого выхода системы y(t). В некоторых случаях входная функция u(t) выбирается таким образом, чтобы усилить влияние неизвестных параметров. Подчеркнем, что в данной ситуации существенным является предположение, что функции f и h, описывающие структуру системы, известны, хотя относительно их линейности никаких предположений не делается.

В качестве иллюстрации задач этого класса рассмотрим задачу о динамике численности некоторой биологической популяции, описание которой может быть получено с помощью следующих логистических уравнений: dx/dt = r x { 1 — (x / K) } — E x, x(0)=x₀.

Здесь x(t) — численность популяции в момент времени t, r — удельная скорость ее роста в отсутствии лимитирования, К — константа, характеризующая предельные трофические возможности среды обитания (уровень насыщения численности), и Е — коэффициент интенсивности изъятия особей из популяции.

Предположим, что имеется возможность измерения численности популяции в каждый момент времени, т.е.

y(t) = x(t),

но численное значение параметра К неизвестно. В этом случае задача идентификации параметров состоит в определении К на основе измерения численности популяции:

K = (-r ⋅ x²) / (dx/dt + (E - r)⋅x)

для всех t>0. Таким образом, для определения К достаточно знать (наблюдать) y(t) на любом интервале времени. Однако в более реальных ситуациях, когда имеется лишь конечное число значений y(t), приходится использовать различные приближенные методы.

Обобщение этой задачи с учетом неопределенности в измерении x(t), наличия различных видов в биологической популяции и т.д. представляют собой достаточно сложные в математическом плане задачи.

Задачи идентификации систем, описываемых с применением более общего аппарата, например, потенциальных функций или теоретико-множественных отношений, пока еще слабо изучены. В отличие от внутреннего или внешнего описания на языке дифференциальных уравнений описания данного типа в гораздо большей степени зависят от того, как сам исследователь представляет себе существо изучаемого процесса. Поэтому в этом случае решение задачи идентификации — больше искусство, чем наука, и состоит в основном в выделении таких множеств и отношений, которые приводят к содержательным результатам.

Ограничения

Системный анализ, как и политика, — это прежде всего искусство действовать в пределах «возможного». Рассматривая математическую формулировку той или иной задачи, исследователь (или лицо, принимающее решение) должен полностью представлять себе те внутренние и внешние факторы, которые могут ограничить его выбор стратегий управления. Различные обстоятельства, связанные с объемом имеющихся ресурсов, способом, который необходимо удовлетворить, имеющейся технологией, наличием и возможностями ЭВМ, людскими ресурсами, бюджетом времени и т.д., резко сужают круг возможностей, доступных исследователю.

Выделим два принципиально различных типа ограничений:

1. внутренние — ограничения, налагаемые структурой самой системы,
2. внешние — ограничения, налагаемые на поведение системы внешними факторами.

Рассмотрим эти ограничения несколько подробнее.

Внутренние ограничения возникают вследствие определенной ограниченности возможностей измерять характеристики состояния системы и управлять течением процесса, т.е. они ограничивают взаимодействие системы с внешним миром. Вообще говоря, ограничения этого типа наиболее четко видны тогда, когда для внутреннего описания используют дифференциальные или разностные уравнения. Для иллюстрации понятия «внутренние ограничения» рассмотрим пример из области биомедицины.

Пример

Фармакокинетика. Предположим, что пациент, страдающий заболеванием сердца, получает дигитоксин, который в результате процесса обмена веществ превращается в дигоксин. Поскольку последний имеет возможность накапливаться в организме, что в результате может привести к летальному исходу, то очень важно уметь точно определять его содержание в организме прежде чем пациент примет очередную порцию дигитоксина.

Многокомпонентная модель, используемая для описания кинетики и превращений дигитоксина, изображена на рис.6.1.

Обычно принято считать, что если в организм вводится некоторая доза дигитоксина, то примерно 92% этой дозы немедленно разносится по организму и около 85% от оставшихся 8% сразу превращается в дигоксин. Предполагается, что динамика концентрации лекарств X и Y может быть описана следующим образом:

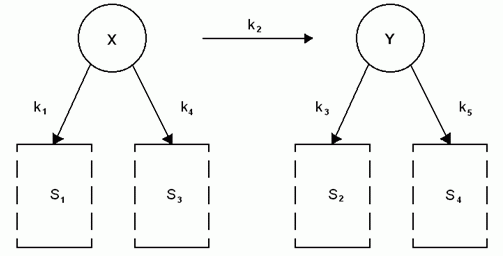
Рис.6.1 — Многокомпонентная структура процесса обмена веществ.

Здесь Х — содержание дитоксина в организме, Y — содержание дигоксина, S₁ и S₂ — мочевые выделения, S₃ и S₄ — немочевые выделения, k_i — коэффициенты диффузии, i = 1,2,3,4,5.

dX/dt = - (k₁ + k₂ + k₄)⋅X,
dY/dt = k₂⋅X - (k₃ + k₅)⋅Y,
dS₁/dt = k₁⋅X,
dS₂/dt = k₃⋅Y,
dS₃/dt = k₄⋅X,
dS₄/dt = K₅⋅Y.

Начальные условия имеют вид:

X(0) = 0,92⋅D,
Y(0) = (0,85)⋅(0,08)⋅D,
S₁(0) = S₂(0) = S₃(0) = S₄(0) = 0,

где D — введеная доза дигитоксина.

Предположим, что можно измерить содержание дигитоксина и дигоксина только в мочевых выделениях. Тогда выход системы имеет вид y₁(t) = S₁(t), y₂(t) = S₂(t).

Именно это весьма реалистическое с практической точки зрения ограничение и является тем, что называется внутренним ограничением системы. В силу этого ограничения не все внутренние переменные системы доступны для непосредственного измерения. Имея в виду основную задачу, стоящую перед врачом, необходимо знать, достаточны ли измерения переменных y₁ и y₂ для определения неизвестной начальной дозы лекарства D. Эта задача является так называемой задачей наблюдаемости, обсуждение которой выходит за рамки настоящего примера.

Внешние ограничения имеют качественно иной характер. Как отмечалось выше, они обусловлены не физическими или структурными ограничениями самого процесса, а «произволом» лица, принимающего решения, которое является «внешним» по отношению к системе. Вообще говоря, эти ограничения связаны с такими обстоятельствами, как ограниченность имеющихся ресурсов и производственных мощностей, наличие заданного спроса и т.д.

Существенным моментом здесь является то, что эти ограничения налагаются извне и не имеют никакого отношения к математическим ограничениям, содержащимся в самой модели. Типичные примеры внешних ограничений содержатся в задачах экономического управления, где требуется определить соответствующее распределение фиксированных финансовых средств для достижения определенных целей. Возьмем, к примеру, сотрудника некоторой компании, ответственного за рекламу ее продукции, причем бюджет, который компания выделила на рекламные цели, составляем М $. Это значит, что он может истратить М $. на размещение рекламных объявлений, скажем, в газетах, журналах, на телевидении, радио и рекламных афишах. Предположим, что вложение x_i $ в i-тый способ рекламы (i — газеты, журналы и т.д.) приводит к сбыту партии объема f_i(x_i) , причем функции f_i(.) считаются известными. Поскольку компания заинтересована в максимизации сбыта, рекламодатель сталкивается с решением задачи максимизации f_i(x_i)по всем распределениям {x_газ, x_журн, x_рад, x_тв, x_аф} при внешнем ограничении

∑x_i ≤ M

Следовательно, внешнее ограничение возникло из-за ограниченности бюджета, а не из-за образа взаимодействия системы с внешним миром.

В качестве другого примера внешнего ограничения рассмотрим задачу о пилоте, которому необходимо пролететь из пункта А в пункт В за минимальное время. В зависимости от характеристик самолета и других предположений, математическое решение этой задачи может привести к оптимальной траектории, показанной на рис.6.2 б). Очевидно, что такое решение не учитывает реальных ограничений, имеющихся в этой ситуации, которые должны быть наложены извне с тем, чтобы сделать задачу осмысленной с физической точки зрения. Надлежащее внешнее ограничение (y > 0) привело бы только к оптимальной траектории, представленной на рис.6.2 а).

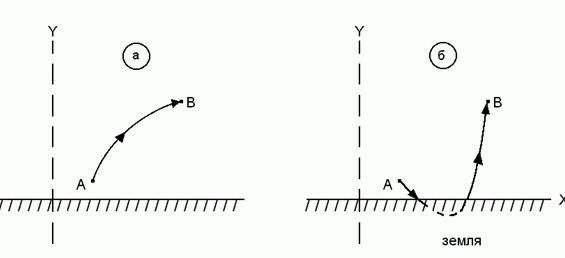
Рис.6.2 — Траектория полета самолета.

Оптимизация

Одна из наиболее злободневных проблем анализа систем, рассматриваемых в сициально-экономических задачах, — это проблема выбора критерия, т.е. вопрос о том, каким образом следует сравнивать между собой различные реализации поведения систем. К счастью, динамические процессы, наблюдаемые в физических и биологических системах, часто протекают по вполне определенным законам, которые, как правило, являются следствием различных принципов минимума или законами сохранения. Однако перенос этих законов на объекты социальной природы в лучшем случае носит искусственных характер и, более того, часто просто невозможен. Поскольку цель нашего курса состоит в изучении структуры систем независимо от вопросов оптимизации, можно позволить себе роскошь оставить в стороне проблему выбора критерия. Тем не менее, для того, чтобы продемонстрировать значимость этой проблемы, рассмотрим простой пример, иллюстрирующий ситуацию, когда выбор различных критериев приводит к качественно различным стратегиям управления.

Предположим, что динамика системы описывается одномерным линейным дифференциальным уравнением dx/dt = u(t), x(0) = c, где u(t) — вход, или функция управления. Предположим, далее, что доступные резервы управления ограничены следующим образом:

|u(t)| ≤ 1 для всех 1 t ≥ 0

(Подобная ситуация возникает, например, при управлении автомобилем, и тогда функция u(t) есть скорость движения.)

Одним из критериев для данного процесса может быть перевод системы из начального состояния с в некоторое заданное состояние, например, x = 0 за минимальное время. Хорошо известно, что решение этой задачи имеет вид:

u(t) = +1, c < 0,
u(t) = -1, c > 0

т.е. релейное управление является оптимальным. Предположим теперь, что мы стремимся минимизировать квадратичный функционал этого вида вида. Можно показать, что в этом случае оптимальный закон управления имеет вид u(t) = th(T-t)⋅x(t),

и он может быть реализован в виде обратной связи или синтеза.

Полученные результаты показывают, что изменение критерия качественно меняет характер решения. В первом случае мы имеем экстремальные управления, переключающиеся с одной границы на другую в зависимости от начального состояния. Во втором случае оптимальный закон управления строится по ходу развития самого процесса и не имеет никаких точек разрыва. Важно отметить, что, хотя динамика системы остается неизменной, выбор иного критерия приводит к качественному изменению оптимального управления.

Стохастические системы.

Несмотря на то, что основная направленность данного курса лекций такова, что не возникает необходимости в подробном обсуждении вопросов, связанных с неопределенностью, тем не менее следует иметь в виду, что при анализе большинства реальных системных задач практически ничего не известно достоверно. Независимо от выбранного математического описания, неопределенности будут присутствовать в динамике, целях, ограничениях и т.п. При удачном стечение обстоятельств для неопределенных переменных будут известны с определенной достоверностью распределения вероятностей. Однако довольно часто даже распределение вероятностей заранее неизвестны, поэтому возникает адаптивная ситуация. В любом случае нельзя считать анализ законченным без тщательного исследования неопределенностей, присущих выбранной модели.

В дальнейшем будем придерживаться довольно смелого предположения, что всеми неопределенными эффектами можно пренебречь, т.е. будем считать, что передаточные функции, динамика состояний и т.д. известны достоверно. Такое допущение, естественно, должно быть оправдано полученными результатами, что мы и попытаемся продемонстрировать в каждом отдельном случае.

↑	Оглавление
←	Лекция 5, «Математическое описание систем» (2 часть)	Лекция 7, «Основные положения теории систем» (1 часть)	→