«Системный анализ и проектирование»

Е. Н. Живицкая

↑	Оглавление
←	Лекция 17, «Методология решения неструктуризованных проблем»	Лекция 19, «Основы принятия решений при многих критериях»	→

Лекция 18: Методология решения слабо структуризованных проблем

Категория целей в системном анализе

Системный анализ начинается с выявления и обоснования конечной цели, которую стремятся достичь при решении возникшей проблемы.

Цель выступает обычно, как прообраз будущего и обозначает некоторый конечный результат, заранее мыслимый и желаемый. Структуризация конечной цели позволяет определить стратегию ее достижения, и именно в этом состоит практическая ценность данной категории.

В процессе формирования конечной цели могут участвовать: эксперты, системные аналитики и ЛПР.

Множество возможных целей.Множество конкретных целей.

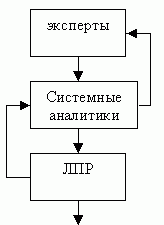
Рис.18.1 — Конечная цель

Все цели принятно разделять на 3 класса:

1. Функциональные цели, способ достижения которых известен и которые уже достигались в данной системе (выполнение производственного плана). Выпуск дипломированных специалистов.
2. Цели-аналоги, которые достигались какой-либо системой,однако никогда не достигались данной системой.Создание ЛВС; создание работизированной технологической линии.
3. Цели развития или новые цели, которые никогда и никакой системой ранее не достигались: создание ОГАС (общегосударственной системы у-я); создание ЭВМ 5 поколения и др.

Для генерации целей могут служить различные способы:

• натурные эксперименты;
• математическое моделирование;
• правдоподобное рассуждение.

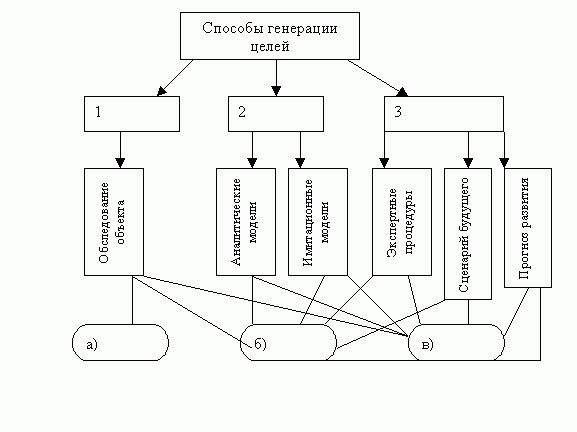
Рис.18.2 — Способы генерации целей

1. натуральные экспериментыа) функциональные цели
2. математическое моделированиеб) цели-аналоги
3. правдоподобные рассужденияв) цели — развитие

Структуризация конечной цели в виде дерева целей

Дерево целей представляет собой многоуровневый граф, отражающий иерархию частных целей и задач, возникающих в результате структуризации конечной цели. При этом процесс структуризации конечной цели опирается на 3 базовых принципа:

1. Стратегия достижения конечной цели из самой цели в результате ее декомпозиции.
2. В процессе декомпозиции конечная цель разбивается на подцели, затем каждая из подцелей разбивается на более простые цели и т.д.

3. Декомпозиция конечной цели осуществляется до уровня таких задач, которые возможно решить и с которых возможно начать операцию по достижению конечных целей. В качестве примера структуризации конечной цели может служить дерево целей в методе ПАТТЕРН.

Действия в Персидском заливе:

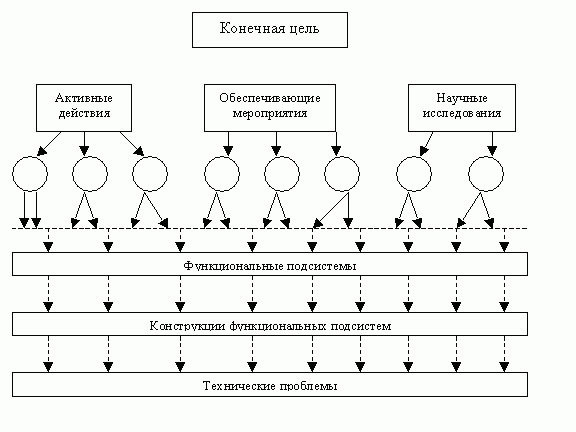
Рис.18.3 — Дерево целей

Дополнительную информацию о дереве целей дает следующая таблица:

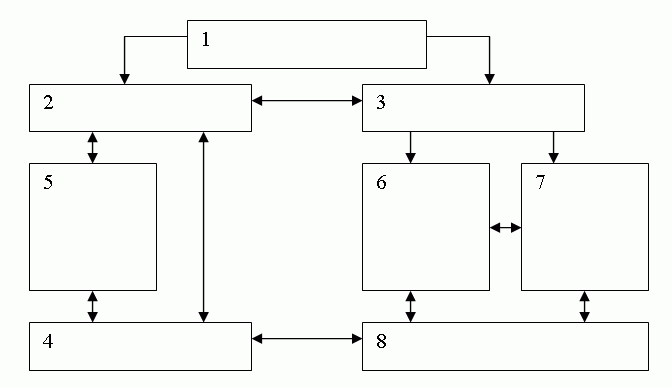
Рис.18.4.

Уровень иерархии	Наименование уровня	Количество элементов
0	Национальные цели	1
1	Мероприятия	3
2	Задачи	8
3	Задания	46
4	Принципы систем	161
5	Функциональные подсистемы	425
6	Конструкции функциональных подсисистем	850
7	Технические проблемы	1987

Особенности построения целевых комплексных программ

Целевая комплексная программа (ЦКП) — это одна из форм реализации программно-целевого метода, который

получает широкое распространение для решения крупных народно-хозяйственных проблем. Каждая ЦКП имеет 3 характерных признака:

1. Направлена на определенный конечный результат.
2. Учитывает множество факторов, необходимых для достижения цели.
3. Представляет собой организованную совокупность мероприятий, позволяющих перевести некую систему из настоящего состояния в желаемое будущее состояние.

ЦКП «АСУ ГПС-90» — занимается ЦПИИТУ:

ЦКП имеют обычно цели-аналоги или цели-развитие:

1. Создание и вывод в действие головных объектов в новой технике.
2. Создание и внедрение АСУ различных уровней, САПР и ВЦКП.
3. P_азработка и внедрение в производство высокоэффективных технологических процессов.
4. Создание и освоение в производстве новых видов машин, оборудования и продуктов.
5. Создание и внедрение методов и средств охраны окружающей среды.
6. Решение проблем, связанных с развитием принципиально новых направлений науки и техники и др.

ЦКП отличаются существенно от традиционных программ:

N	Системные характеристики	Система для достижения конечной цели
		Традиционные программы	Целевая комплексная программа (ЦКП)
1	Конечная цель	Задается	Задается; структура цели — формируется
2	Организационная структура	Задается	Формируется
3	Ресурсы материальные и др.	Pаспределяются	Формируются
4	Время достижения цели	Задается	Приближенные оценки
5	Внешняя среда	Не является объектом выбора	Формируется

Основные методы научно-технического прогнозирования

Прогнозирование — это процесс формирования вероятного суждения о будущем состоянии некоторого объекта на основе анализа тенденции его развития. Наличие прогноза позволяет избежать ошибочных, преждевременных или запоздалых решений, что весьма важно для ускорения темпов научно-технического развития. Прибыль, получаемая от систематического внедрения прогнозов, в 50 раз превышает затраты на прогнозирование (это определили Давыдов и Лисичкин).

Все известные методы прогнозирования можно разбить на 4 группы:

1. Методы, которые базируются на фактографической информации, представленной обычно в виде временныхрядов.
2. методы, которые базируются на эвристической информации, полученной от высококвалифицированных специалистов.
3. Методы, которые основаны на принципе аналогии: биологической, исторической или математической.
4. Комплексные методы, которые основаны на сочетании различных методов прогнозирования и средств реализации.

1-й. Например, мы обладаем данными по средней мощности автомобиля с 1901...до 1987г. Какая будет в 2002 г?

2-й. Метод Дельфи — метод экспертных оценок, например, «сколько надо выпускать компьютеров в следующем году?».

4-й. К числу перспективных комплексных методов относятся: метод Паттерн (США,1964г) и метод прогнозного графа (СССР, 1969г). Оба метода служат для обеспечения плакирования и управления разработками крупных программ.

Метод Паттерн постоянно применяется в США в области вооружения, космических исследований и медицины. Практическое использование метода начинается с составления сценария, т.е. документа, в котором анализируются национальные цели, направления усилий и задачи на перспективу. На основе сценария дерево целей и находятся коэффициенты относительной важности для всех его элементов. Одновременно осуществляется прогноз научно-технического развития, и на его основе определяются:

1. Коэффициенты, характеризующие состояние и сроки разработки.
2. Коэффициенты, характеризующие полезность разработок в других областях.

С помощью ЭВМ определяются прогнозные оценки на заданный момент времени с учетом всех коэффициентов.

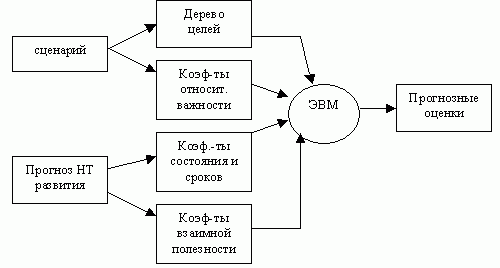
Рис.18.5 — Прогнозные оценки

Метод прогнозного графа дает возможность прогнозировать те или иные события, время и вероятность их наступления. Основой метода является прогнозный граф, отражающий суждение экспертов в отношении конечной цели, путей ее достижения и имеющихся ресурсов. Граф может насчитывать несколько тысяч событий и содержит множество путей достижения конечной цели. Обработка информации на ЭВМ позволяет оценить различные пути на графе и выбрать решение, оптимальное по стоимости, времени и другим критериям. С помощью соответствующих программ осуществляется перестройка графа, его упорядочение и обновление. По мере поступления новой информации выполняется переоценка путей достижения конечной цели.

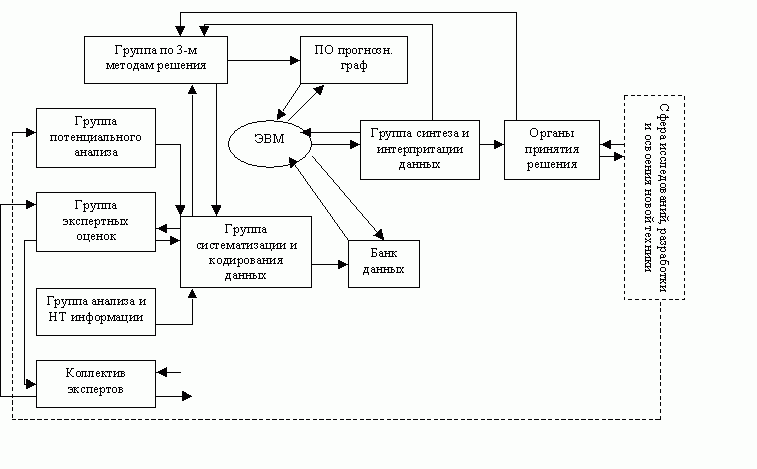
Рис.18.6 — Переоценка путей достижения конечной цели

Поиск новых технических решений на основе морфологического анализа

Для высшего качества проработки технических решений служит новый класс методов — методы поиска новых технических решений.

К числу перспективных относится метод морфологического ящика Ф Цвикки, позволяющий систематизировать <возможные технические решения и выбрать из их числа рациональные решения. При этом синтезируются как известные, так и новые технические решения, которые при несистематизированной деятельности вообще могут быть упущены.

Одна из модификаций метода состоит в следующем:

1. Определяется целевое назначение искомого технического объекта
2. Исходя из целевого назначения объект разделяется на важнейшие функциональные узлы
3. Для каждого функционального узла, независимо от других узлов, находится множество технических решений
4. Состоится морфологическая матрица, содержащая возможные технические решения
5. На основе матрицы выбирается техническое решение для объекта в целом

Дадим иллюстрацию метода на примере выбора рациональной структуры КТС АСУ на предпроектной стадии:

1. Своевременное поступление качественной информации для принятия решения

2. Функциональные узлы:

   • P₁ — регистрация и сбор информации;
   • P₂ — передача информации;
   • P₃ — подготовка информации;
   • P₄ — ввод информации;
   • P₅ — обработка информации;
   • P₆ — вывод информации.

3. Технологические решения

   P₁ → P₁¹, P₁², ...

   P₂ → P₂¹, P₂², ...

   ...

   P₆ → P₆¹, P₆², ...

   т.е. есть функциональный узел P₁ и для него мы определяем множество возможных решение и т.д

4. Морфологическая матрица. Матрица потенциально содержит множество структур. Предположим, что нас устраивает O. Соединим O и получим вариант структуры КТС.

5. P_ациональная структура.

Проектирование систем с использованием системных принципов

Задача: пусть объектом проектирования является система телекодовой радиосвязи, которая предназначена для помехоустойчивой передачи двоичной информации от источника к получателю.

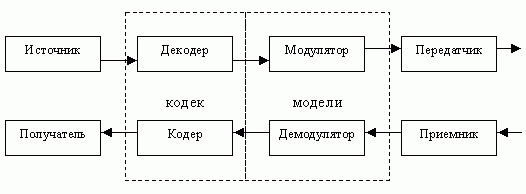
Рис.18.7 — Система телекодовой радиосвязи

Кодер — обладает корректирующим свойством (внесением дополнительных символов). Выбираем все, кроме приемника. Известна матрица альтернативных технических средств. Эта матрица уже упорядочена.

Тип	Избыточность кода R	Стоимость	Тип	Пропускная способность I бит/сек	Стоимость	Тип	Мощность передатчика P (КВт)	Стоимость
K0	0	0	M1	600	C(M1)	П1	5	C(П1)
			M2	1200	C(M2)	П2	15	C(П2)
K0	0	0	M3(1)	1200	C(M3)	П3	25	C(П3)
K1	1/2	C(K1)	M3(2)	2400
K0	0	0	M4(1)	1200	C(M4)	П4	60	C(П4)
K1	1/2	C(K1)	M4(2)	2400
K2	3/4	C(K2)	M4(3)	4800

C(K₁) < C(K₂), C(M₁) < C(M₂) < C(M₃) < C(M₄), C(П₁) < C(П₂) < C(П₃) < C(П₄), т.к. мы выбираем по интуиции.

Матрицу составили в порядке изменения характеристик.

!Стоимость — дело соглашения. Выбирать только по стоимости не целесообразно. Выбор нужно производить по техническим требованиям.

Требуется найти оптимальный по стоимости вариант системы, который обеспечивает передачу информации со скоростью V = 1200бит/сек и вероятность ошибки не более, чем P_ош = 0,001 (т.е. 1 ошибка на 1000 передаваемых символов).

1. Традиционный подход предусматривает выбор самых дешевых кодека, модема и передатчика, исходя из заданных требований к системе.

   Выбор кодека: K₀ → C(K₀) = 0

   Выбор модема: M₂ → C(M₂)

   Выбор передатчика: P_ош = f(P) или f(P) = 10-3

   Эту мощность обеспечивает только П₄ — С(П₄)

   В результате выбора имеем:

   В_опт = (K₀, M₂, П₄) (*)

   С = С(M₂) + С(П₄)

   Вариант системы со звездочкой не является opt, т.к. стоимость системы по этому варианту не является минимальной, хотя на каждом из этапов выбиралось самое дешевое решение.

2. Системный подход предусматривает отбор допустимых вариантов системы, исходя из заданных требований, оценку этих вариантов по стоимости и выбор варианта с минимальной стоимостью.

3. Отбираем сочетание кодеков и модемов по заданной скорости передачи информации V_пер = (1-R)⋅I = 1200 где R — характеристика по модемам, I — пропускная способность по модемам. Данному условию удовлетворяют такие сочетания: (K₀, M₂), (K₀, M₃⁽¹⁾), (K₀, M₄⁽¹⁾), (K₁, M₃⁽²⁾), (K₁, M₄⁽²⁾), (K₂, M₄⁽³⁾)

4. Отобранные сочетания кодеков и модемов проверяем на требования по вероятности ошибки: P_ош = 0,001. Если в i-том решении Р < 60 КВт, то сочетание кодека и модема вместе с соответствующим передатчиком относят к разряду допустимых.
5. Определяем стоимость допустимых сочетаний кодека, модема и передатчика C = C(K_доп) + C(M_доп) + C(П_доп)
6. Выбираем допустимое сочетание кодека, модема и передатчика, оптимальное по критерию стоимости.

В данной задаче оптимальное решение следующее:

В_опт = (K₁, M₄⁽²⁾, П₂) (**)

C = С(K₁) + С(M₄⁽²⁾) + С(П₂)

Вариант системы (**) является оптимальным, т.к. стоимость системы по этому варианту является минимальной,причем система оптимизировалась в целом как единый объект. Каждая система должна оптимизироваться в целом, т.е. как единый объект с заданным целевым назначением, т.к. оптимизация по частям не дает в общем случае оптимальной системы и оправдано лишь в двух типичных ситуациях:

1. Когда части системы независимы по оптимизируемым параметрам (это очень редкий случай);
2. Когда оптимизация системы в целом затруднительна в силу ее сложности или каких-либо других причин.

Организация экспериментов с использованием системных принципов

Предположим, что осуществляется эксперимент по взвешиванию 3-х объектов А, В, С, причем важно выявить процедуру взвешивания, оптимальную по критерию точности.

Традиционный подход к взвешиванию объекта реализуется по следующему плану:

N опыта	Объекты взвешивания			Результаты взвешивания
	A	B	C
1	-1	-1	-1	У1
2	+1	-1	-1	У2
3	-1	+1	-1	У3
4	-1	-1	+1	У4

• -1 — объект отсутствует на весах;
• +1 — объект присутствует на весах.

Согласно плану, сначала осуществляется холостое взвешивание, а затем поочередно взвешивается каждый из объектов. При этом вес объекта определяется по результатам 2-х опытов:

А = У₂-У₁

В = У₃-У₁

С = У₄-У₁

Определим дисперсию определения веса объекта А

D[A] = D[У₂-У₁] = D[(m₂+E₂)-(m₁+E₁)] = D[(m₂-m₁)+(E₂-E₁)] =  = D[m₂-m₁]+D[E₂-E₁] = D[E₂]+D[-E₁] = D[E₂]+(-1)2D[E₁] = 2⋅D[E],

где D[E] — дисперсия случайной ошибки взвешивания

D[A] = 2⋅D[E]
D[B] = 2⋅D[E]	(*)
D[C] = 2⋅D[E]

Системная процедура взвешивания реализуется по следующему плану:

N опыта	Объекты взвешивания			Результаты взвешивания
	A	B	C
1	+1	+1	+1	У1
2	+1	-1	-1	У2
3	-1	+1	-1	У3
4	-1	-1	+1	У4

Согласно плану, сначала осуществляется взвешивание всех объектов, а затем последовательно взвешивается каждый из объектов. При этом вес объектов определяется по результатам каждого из 4-х объектов:

A = (У₁ + У₂ - У₃ - У₄)/2

B = (У₁ - У₂ + У₃ - У₄)/2

C = (У₁ - У₂ - У₃ + У₄)/2

2» — т.к. мы как бы дважды «взвесили колбасу».

Определим дисперсию веса объекта А

D[A] = D[(У₁ + У₂ - У₃ - У₄)/2] =
= 1/4⋅D[У₁ + У₂ - У₃ - У₄] =
= 1/4⋅D[(m₁ +E₁) + (m₂ +E₂) - (m₃ +E₃) - (m₄ +E₄)] =
= 1/4⋅D[(m₁ + m₂ - m₃ - m₄) + (E₁ + E₂ - E₃ - E₄)] =
= 1/4⋅D[m₁ + m₂ - m₃ - m₄] + 1/4⋅D[E₁ + E₂ - E₃ - E₄] =
= 1/4⋅{D[E₁] + D[E₂] + D[-E₃] + D[-E₄]} = 1/4⋅4⋅D[E] = D[E]

D[A] = D[E]
D[B] = D[E]	(**)
D[C] = D[E]

Сравнение * и ** приводит к выводу: системная процедура взвешивания обеспечивает удвоение точности по сравнению с традиционной процедурой.

Примеры: попытка найти угол в комнате, ближайшей к вершине. Традиционная процедура базируется на концепции однофакторного эксперимента, причем вес объекта определяется по результатам 2-х опытов. Системная процедура реализует концепцию многофакторного эксперимента и предусматривает определение веса объекта по результатам всех 4-х опытов. Т.о. выигрыш в точности получен за счет организации многофакторного эксперимента.

Переоценка альтернатив на основе Байесовского подхода

P_ассмотрим множество альтернатив H₁, H₂, ..., H_n, образующих полную группу несовместных событий. Известны априорные вероятности альтернатив Р(H₁), Р(H₂), ..., Р(H_n)

Производится некоторый эксперимент, в результате которого происходит событие А, причем возможно найти условные вероятности события А.

Р(А/H₁), Р(А/H₂), ..., Р(А/H_n)

В этих условиях апостериорные (послеопытные) вероятности альтернатив определяются формулой Байеса:

P(H_l/A) = [P(H_l)⋅P(A/H_l)]/∑[P(H_l)⋅P(A/H_l)]

Формула Бейеса позволяет осуществить переоценку альтернатив с учетом дополнительной информации, поступающей в результате эксперимента. Наличие дополнительной информации уменьшаетаприорную неопределенность.Поэтому степень доверия к апостериорным вероятностям должна быть больше,чем к соответствующим априорным вероятностям.

Пусть требуется оценить надежность изделий, которые производятся некоторой фирмой. Фирма заявляет, что надежность изделий = 98%. Надежность оценивается также агенством, осуществляющим испытание изделий.Агенство утверждает, что надежность изделий составляет 90%. Заказчик, покупающий изделие, сомневается в оценке над-ти изделий фирмой и агенством. Согласно субъективному мнению заказчика, вероятность того, что заявление фирмы верно, равно 0,4, а вероятность того, что верно утверждение агенства, равно 0,6. С целью уменьшения априорной неопределенности, заказчик осуществляет испытание i-тых изделий.

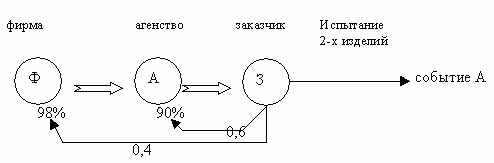
Рис.18.8 — Испытание изделий

В данной задаче имеем 2-х альтернативную ситуацию.

H₁ = (P_ф = 0,98)

H₂ = (P_а = 0,9)

Известны априорные вероятности альтернатив, отражающие субъективное мнение заказчика.

Р(H₁) = Р(P_ф = 0,98) = 0,4

Р(H₂ = Р(P_а0,9) = 0,6

В результате испытания 2-х изделий могут быть события: А, В или С.

А — 2 неудачи; В — 1 неудача, 1 успех; С — 2 успеха.

Предположим, что в результате испытаний произошло событие А. Найдем условие вероятности события А.

Р(А/H₁) = Р(неудача при 1-ом испытании/H₁)⋅Р(неудача при 2-ом испытании/H₁) =
= (1-0,98)⋅(1-0,98) = 0,0004

Р(А/H₂) = Р(неудача при 1-ом испытании/H₂)Р(неудача при 2-ом испытании/H₂) =  = (1-0,9)⋅(1-0,9) = 0,01

Теперь возможно осуществить переоценку исходных альтернатив

P(H₁/A) = [P(H₁)⋅P(A/H₁)]/∑[P(H_l)⋅P(A/H_l)] = ... = 0,03

P(H₂/A) = [P(H₂)⋅P(A/H₂)]/∑[P(H_l)⋅P(A/H_l)] = ... = 0,97

С вероятностью 0,97 можно утверждать, что надежность изделия составляет 90%.

Процедура структуризации проблемы в виде дерева решений

Пусть требуется выбрать оптимальную стратегию для некоторой организации, которая желает установить дорогостоящее оборудование зарубежного производства.

Исправность оборудования могут оценить приглашенные специалисты, услуги которых необходимо оплачивать. Если они не приедут, то решить этот вопрос затруднительно. Конечно, можно дождаться их приезда, однако в одном случае возможны задержки с установкой оборудования, что сулит организации неприятности. К тому же организация не очень-то доверяет оценкам специалистов. По мнению организации, вероятность того, что специалисты правильно оценивают исправность оборудования = 0,7. Согласно оценки организации, вероятность исправного состояния оборудования не превышает 0,4.

Для структуризации проблемы в виде дерева решений рекомендуется следующая процедура:

1. Составляется список всех возможных экспериментов {e}, которые могут быть осуществлены.

   e₁ — ожидать приезда специалистов;

   e₂ — устанавливать оборудование своими силами;

2. Составляется список всех возможных результатов{z}, которые получают после осуществления экспериментов

   z₁ — по оценке специалистов оборудование исправно;

   z₀ — по оценке специалистов оборудование не исправно;

   z_н — неопределенность.

3. Составляется список всех возможных операций {a}, которые предпринимаются после получения результатов эксперимента.

   a₁ — проверить исправность оборудования;

   a₀ — не проверять исправность оборудования.

4. Составляется список всех возможных состояний {Q}, которыми характеризуется оборудование в действительности.

   Q₁ — оборудование исправно;

   Q₀ — оборудование неисправно.

5. На основе данных пунктов 1-4 разрабатывается многоальтернативный граф, который представляет собой дерево решений.

   U₁ = U(e₁, z₁, a₁, Q₁)

   U₂ = U(e₁, z₁, a₁, Q₀)

   .....................

6. Строится дерево.

Выбор оптимальной стратегии на основе байесовской теории решений

Согласно байесовской теории решений, осуществляются следующие процедуры: прежде всего, по каждому маршруту дерева решений определяется возможный выигрыш; затем находятся априорные и апостериорные вероятностные распределения; наконец, выполняются необходимые расчеты, позволяющие выбрать оптимальную стратегию.

1. Оценивается значение каждого выигрыша U(e, z, a, Q), который представляется в виде суммы 2-х частей = U(e,z)+U(a,Q), где

   U(e,z)	z1	z0	zн
   e1	-3	-3
   e0			0

    

   U(a,Q)	Q1	Q0
   a1	0	5
   a0	8	-10

2. 3 — тратим 3000 руб. Перебирая все возможные матрицы на дереве решений, получаем:

   U₁ = U(e₁, z₁, a₁, Q₁) = -3 + 0 = -3

   U₂ = U(e₁, z₁, a₁, Q₀) = -3 + 5 = 2

   U₃ = ... = 5

   U₄ = ... = -13

   U₅ = ... = -3

   U₆ = ... = 2

   U₇ = ... = 5

   U₈ = ... = -13

   U₉ = ... = 0

   U₁₀ = ... = 5

   U₁₁ = ... = 8 — наибольший выигрыш, но эти оценки ... и им доверять нельзя

   U₁₂ = ... = -10

3. Исходя из содержания задачи, определяются априорные вероятности P(Q) P(Q₁) = 0,4 — «рыхлая» субъективная вероятность; P(Q₀) = 0,6

4. Исходя из содержания задачи, определяются условные вероятности: P(z/e,Q)

   P(z₁/e₁, Q₁) = 0,7 — вероятность правильной оценки состояния оборудования

   P(z₀/e₁, Q₁) = 0,3 — вероятность ошибочной оценки состояния оборудования

   P(z₁/e₁, Q₀) = 0,3

   P(z₀/e₁, Q₀) = 0,7

   P(z_n/e₀, Q₁) = 1 — вероятность достоверного события

   P(z_n/e₀, Q₀) = 1 — (специалисты не приехали)

   Т.е. перебрали все возможные варианты условных вероятностей.

5. По формуле Байеса вычисляются апостериорные вероятности

   P(Q₁/e₁,z₁) = [P(Q₁)⋅P(z₁/e₁,Q₁)]/[P(e₀)⋅P(z₁/e₁,Q₀) + P(Q₁)⋅P(z₁/e₁,Q₀)] = [0,4⋅0,7]/[0,6⋅0,3 + 0,4⋅0,7] = 0,61

   P(Q₀/e₁,z₁) = [0,6⋅0,3]/[0,6⋅0,3 + 0,4⋅0,7] = 0,39

   P(Q₁/e₁,z₀) = [0,4⋅0,3]/[0,6⋅0,7 + 0,4⋅0,3] = 0,22

   P(Q₀/e₁,z₀) = [0,6⋅0,7]/[0,6⋅0,7 + 0,4⋅0,3] = 0,78

   P(Q₁/e₀,z_н) = P(Q₁) = 0,4

   P(Q₀/e₀,z_н) = P(Q₀) = 0,6

6. Для каждой комбинации (e,z) находится ожидаемый выигрыш от осуществления возможных операций а.

   U(e,z,a) = ∑U(e,z,a,Q)⋅P(Q/e,z)

   U(e₁,z₁,a₁) = U(e₁,z₁,a₁,Q₀)⋅P(Q₀/e₁,z₁) + U(e₁,z₁,a₁,Q₁)⋅P(Q₁/e₁,z₁) = 2⋅0,39 + 3⋅0,61 = -1,05

   U(e₁,z₁,a₀) = -13⋅0,39 + 5⋅0,61 = -2,02

   U(e₁,z₀,a₁) = 2⋅0,78 + 3⋅0,22 = 0,9

   U(e₁,z₀,a₀) = -13⋅0,78 + 5⋅0,22 = -9,04

   U(e₀,z_н,a₁) = 5⋅0,6 + 0⋅0,4 = 3

   U(e₁,z_н,a₀) = -10⋅0,6 + 8⋅0,4 = -2,8

7. Для каждой комбинации (e,z) находится максимальный выигрыш и оптимальная операция.

   U(e,z)_max = max(a{U(e,z,a)}) → a_opt

   U(e₁,z₁)_max = max(a{U(e₁,z₁,a₀);U(e₁,z₁,a₁)}) = max(a{-2,02;-1,05}) = -2,02 → a_opt = a₁

   U(e₁,z₀)_max = max(a{-9,04;0,9}) → a_opt = a₁

   U(e₀,z_н)_max = max(a{-2,8;3}) → a_opt = a₁

8. Определяются вероятности P(z/e), которые описывают результаты всех возможных экспериментов z

   P(z₁/e₁) = P(Q₀)⋅P(z₁/e₁,Q₀) + P(Q₁)⋅P(z₁/e₁,Q₁) = 0,6⋅0,3 + 0,4⋅0,7 = 0,46

   P(z₀/e₁) = 0,6⋅0,7 + 0,4⋅0,3 = 0,54

   P(z_н/e₀) = 1

9. Определяется ожидаемый выигрыш U(e) для каждого эксперимента E:

   U(e) = ∑U(e,z)_max⋅P(z/e)

   т.е. это формула для максимального ожидания. Сворачиваем «хвостики» = 0,9⋅0,54 - 1,05⋅0,46 = 0,003

   Таким образом, оптимальная стратегия состоит в том, чтобы устанавливать оборудование силами организации, предварительно проверив его исправность.

10. Находится максимальный выигрыш U(e)_max и оптимальный эксперимент e_опт

    U(e)_max = max(e{U(e)}) → e_опт

    U(e)_max = max(e{U(e₀);U(e₁)}) =max(e{3;0,003}) = 3 → e_опт = e₀

Критерий для оптимизации решений в условиях риска и неопределенности

Процесс оптимизации решений может осуществляться в следующих условиях:

1. Определенности, когда имеется достоверная информация о состоянии внешней среды.
2. Риска, когда возможно задеть вероятностное распределение для состояний внешней среды.
3. Неопределенности, когда о состояниях внешней среды есть лишь общие представления.
4. Противодействие, когда внешнюю среду представляет сознательный противник.

Самые интересные 2 и 3 класса — самые правдоподобные. Операции, проводимые в условиях риска и неопределенности, принято называть играми с природой. Для этих операций характерно наличие неполноты информации в отношении внешней среды (числа пользователей системы, спроса на продукцию, климатических условий и др.). Типичная игра с природой состоит в выборе opt. Стратегии opt, если имеется m конкурирующих стратегий X_j и n состояний природы S_i, причем известна матрица выигрышей a_ji.

Xi/Si	S1	S2	...	Sn
X1	a11	a12	...	a1n
X2	a21	a22	...	a2n
...	...	...	...	...
Xm	am1	am2	...	amn

В некоторых случаях вместо матрицы выигрышей оперирует матрицей рисков, которая содержит множество рисков.

Z_ji = max_ji(a_j) - a_ji

Смысл: риск — это потеря выигрышей. Покажем на примере, как перейти от матрицы выигрышей к матрице риска.

aji S1 S2 S3 S4 X1 1 4 5 9 X2 3 8 4 3 X3 4 6 6 2

→

Zji S1 S2 S3 S4 X1 3 4 1 0 X2 1 0 2 6 X3 0 2 0 7

Для оптимизации решений в условии риска применяются критерии Критерий max среднего выигрыша:

K₁ = max(a_j) = max(∑a_ji⋅P_i)

Критерий минимума:

K₁ = min(z_j) = min(∑z_ji⋅P_i)

Найдем оптимальные стратегии, пологая:

P₁ = 0,1; P₂ = 0,2; P₃ = 0,5; P₄ = 0,2 — это вероятности воздействия внешней среды.

Применяя критерии K₁ и K₂, получаем:

применяем K₁: K₁ = max({5,2; 4,5; 5}) = 5,2 → x_opt = x₁

т.е. 0,1⋅1 + 0,2⋅4 + 0,5⋅5 + 0,2⋅9

K₂: K₂ = min({1,6; 2,3; 2,8}) = 1,6 →  x_opt = x₁.

Стратегия, максимизирующая средней выигрыш, совпадает со стратегией, минимизирующей средний риск. Т.е. на практике можно использовать любую из матриц: либо матрицу выигрышей, либо матрицу рисков. Для оптимизации решений в условиях неопределенности служат следующие критерии:

1. Критерий Лапласса:

   К_Л = max((1/n)⋅∑a_ji)

2. Максиминный критерий Вальда:

   К_В = max(X_j)⋅min_Si(a_ji),

   который ориентируется на худшее состояние внешней среды и выбирает стратегию с максимальным выигрышем (критерий крайнего пессимизма)

3. Мини-максный критерий Сэвиджа:

   К_С = min(X_j)⋅max(S_i⋅Z_ji),

   который ориентируется на самую неблагоприятную обстановку и выбирает стратегию с минимальным риском (критерий крайнего писсимизма).

4. Критерий Гурвица:

   К_Г = max(X_j)⋅[α⋅min(S_i⋅a_ji) + (1 -α)⋅max(S_i⋅a_ji)]

   критерий Гурвица имеет характерные частные случаи:

   • критерий крайнего оптимизма

     К_Г^(2-0) = max(X_j)⋅max(a_Si⋅a_ji)

   • критерий крайнего пессимизма

     К_Г^(2-0) = max(X_j)⋅max(a_Si⋅a_ji) = К_В,

     который основан на выделении 3-х зон в матрице выигрышей, а именно: плохих, промежуточных и благоприятных результатов, получаемых с вероятностями P₁, P₂, P₃.

Выбор рациональной стратегии с использованием многих критериев

Предположим, что некая организация предпочитает иметь ВЦ с распределенной сетью терминалов. С этой целью составляется смета расходов на создание ВЦ с различным количеством терминалов и определяется матрица выигрышей (в тыс. рублей), которые зависят от количества терминалов X_j и числа пользователей S_i

Xj/Si	S1 = 0	S2 = 10	S3 = 20	S4 = 30	S5 = 40	S6 = 50
X1 = 20	-121	62	245	245	245	245
X2 = 30	-168	14	198	380	380	380
X3 = 40	-216	-33	150	332	515	515
X4 = 50	-264	-81	101	284	468	650

Сумма по 1-й строке = 921 921/6 = 153,5

Осуществим выбор рациональной стратегии, используя различные критерии для оптимизации решений в условиях неопределенности.

1. К_Л = max X_j {153, 198, 210, 193} = 210 X_opt = X₃ = 40 — т.е. ВЦ нужно рассчитывать на 40 терминалов

2. К_В = max X_j {-121, -168, -216, -264} = -121

   X_opt = X₁ = 20 — т.е. выбираем минимальный элемент по строке

3. Перейдем от матрицы выигрышей к матрице рисков.

   Xj/Si	S1 = 0	S2 = 10	S3 = 20	S4 = 30	S5 = 40	S6 = 50
   X1 = 20	0	0	0	135	270	405
   X2 = 30	47	48	47	0	135	270
   X3 = 40	95	95	95	48	0	135
   X4 = 50	145	143	144	96	47	0

   К_С = min(X_j {405, 270,135,145}) = 135

   По строчкам; 1-ая строка (max), 2-ая строка max риск. Это означает ориентацию на самую неблагоприятную обстановку.

   X_opt = X₃ = 40

4. Критерий Гурвица. Мы можем по своему усмотрению задать критерий A. Если хотим подстраховаться, то A = 1. Если затрудняемся задать A, то A = 0,5.

   К_Г(A = 0,5) = max(X_j {62,106,150,193}) = 193

   1-ая строка (смотри матрицу выигрышей: min + max/2)

   X_opt = X₄ = 50

5. Выделим 3 зоны в матрице выигрышей: зону плохих результатов, зону промежуточных результатов и зону хороших результатов. Введем субъективные вероятности:

   P₁ = 0,1; P₂ = 0,2; P₃ = 0,7.

   К = {171, 270, 335, 393} = 393

   X_opt = X₄ = 50

   Нами получена следующая совокупность результатов:

   К_Л → 40 терминалов

   К_В → 20 терминалов

   К_С → 40 терминалов

   К_Г → 50 терминалов

   К → 50 терминалов

   Получаем рациональное решение из оптимальных результатов.

   Можно: усреднить эти результаты; отбросить нетипичный результат (20) и взять среднее значение. В качестве рациональной стратегии целесообразно выбрать компромиссное решение: 45 терминалов.

↑	Оглавление
←	Лекция 17, «Методология решения неструктуризованных проблем»	Лекция 19, «Основы принятия решений при многих критериях»	→