«Исследования по общей теории систем»

В.Н. Садовский, Э.Г. Юдин

↑	Оглавление
←	Системы, организации и междисциплинарные исследования (Р. Л. Акоф)	Целое и развитие в свете кибернетики (О. Ланге)	→

Общая теория систем и ее математические основы

М. Д. Месарович (перевод Б. Г. Юдина с рукописи)

Mihajlо D. Мesаrоvic, General Systems Theory and its Mathematical Foundations. Представлено на конференцию по системной науке и кибернетике, организованную Институтом радиоинженеров (Бостон, Массачусетс, 11—15 октября 1967 года).

Введение

Назначение этой статьи — изложить основания математической теории абстрактных систем, рассмотреть ограничения, возникающие в связи с применением математических методов в этой теории, и, наконец, указать области ее применения в технике.

Особо будут подчеркнуты два момента: необходимость простоты и точности при определении основных понятий, так как иначе описание сложной системы может стать неэффективным; четкое выделение целенаправленного подхода, составляющего важный аспект теории систем. Для того чтобы сделать второй момент более явным,эв последнем разделе дано формализованное представление понятия целенаправленной системы.

Настоящую статью можно рассматривать как новый вариант одной более ранней работы автора, поскольку здесь обсуждаются те же основные проблемы и проводится та же точка зрения, что и в работе [1].

1. Что такое математическая теория абстрактных систем?

Мы рассматриваем математическую теорию абстрактных систем как такую теорию математических моделей реально существующих систем¹, в рамках которой основные свойства этих систем исследуются с помощью весьма простых математических структур (согласующихся с интуитивной интерпретацией этих свойств). Такого рода общая теория систем развивается в настоящее время на базе теории множеств и смежных областей абстрактной математики [1]; [2]; [3]; [9]; [10]; [11].

Выбор такого базиса для общей теории систем обусловлен тем, что объекты, изучаемые в математике (независимо от того, какой специальный раздел ее имеется в виду в том или ином конкретном случае), по существу (и в первую очередь), являются множествами и отношениями между множествами и их элементами. Различия между отдельными областями математики определяются главным образом тем, какими дополнительными свойствами (то есть какой «структурой») обладают рассматриваемые множества (и отношения)².

Необходимо провести различение между объектами, изучаемыми в математике, и методом изучения этих объектов. Формализация последнего процесса — область метаматематики, то есть формальной теории дедуктивного вывода в математических дисциплинах. Метаматематика в свою очередь также использует различные математические структуры. Эти структуры выбираются исходя из философских оснований, поэтому они достаточно резко отражают, что именно интуитивно (и на базе философской логики) принимается за дедуктивный вывод. Однако они представляют особый подкласс класса математических структур, и поэтому с чисто абстрактной, формалистической точки зрения им не может быть отдано предпочтение при построении теории поведения различных реально существующих систем. Математические структуры, обычно применяемые в метаматематике, являются финитными, однако в последнее время здесь началось использование более мощных математических методов [4]. Введение в метаматематику нефинитных методов позволило достичь большей простоты и повысило эффективность исследований. Изложенные соображения объясняют, почему в качестве основы общей теории систем используется скорее теория множеств (то есть математика), чем логика (то есть метаматематика).

Рассмотрим теперь некоторые основные понятия и проблемы общей теории систем более детально.

Для данного семейства множеств X = {X₁, ..., X_n} система (абстрактная система) определяется как отношение на X, то есть S ⊂ X₁ × ... × X_n, где «×» обозначает декартово произведение множеств. Множества X₁, ..., X_n, на которых определяется отношение, называются объектами. Каждое X_i представляет полную совокупность всех проявлений некоторого атрибута (или экспериментов с данным атрибутом) рассматриваемых реально существующих явлений. Очевидно, что S представляет собой полную совокупность всех проявлений реально существующей системы (или экспериментов с ней).

В общей теории систем рассматриваются два основных типа проблем.

1. Конструктивный анализ (specification): как построить эффективную процедуру, пригодную для предсказания, то есть как определить некоторые элементы системы, если даны некоторые другие ее элементы. Конструктивный анализ как основа для предсказания поведения систем демонстрирует полезность системных представлений.
2. Анализ системных свойств: как формализовать определенные свойства, существенные для характеристики реально существующих систем, и как эти свойства используются при проведении конструктивного анализа.

Существует два основных способа построения конструктивного анализа систем: терминальный подход и целенаправленный подход.

α) При терминальном подходе объекты, входящие в систему, расчленяются на два класса: X ⊂ X₁ × ... × X_m и Y ⊂ X_m+1 × ... × X_n, так что система в этом случае определяется как S ⊂ X × Y. Объекты из X называются входами (и представляют причину, стимул рассматриваемого явления), тогда как объекты из Y называются выходами (и представляют следствие, реакцию). Конструктивный анализ терминальных систем проводится путем построения дополнительной структуры на множествах-объектах таким образом, чтобы можно было определить более простую систему (в надежде, что мощность этой системы будет конечной) и с ее помощью охарактеризовать исходную систему, например, посредством рекурсивного или индуктивного процесса. Такие сравнительно простые системы, применяемые для конструктивного анализа, называются вспомогательными функциями [2]. Часто они требуют введения в описание систем некоторых новых (вспомогательных) объектов (понятий), наиболее важными из которых являются понятия состояния объекта и пространства состояний [2]; [3].

β) При целенаправленном подходе конструктивный анализ (а вместе с тем и определение самого понятия целенаправленного подхода) достигается благодаря введению представления о цели системы и описанию поведения системы в связи с этой целыо. В последнем разделе этой статьи дается формальное определение целенаправленной системы. Необходимо подчеркнуть, что целенаправленное описание системы требуется не по философским или концептуальным причинам, а скорее, по чисто техническим соображениям для осуществления конструктивного анализа. Целенаправленный подход можно рассматривать также как альтернативный путь имплицитного определения некоторой функции (или отношения): дело в том, что для определенного класса систем конструктивный анализ можно провести лишь в терминах целенаправленного, а не терминального подхода. Это не значит, конечно, что основные понятия, используемые при терминальном описании систем (например, понятие состояния объекта), не могут быть строго определены; проблема здесь состоит в том, что совокупность вспомогательных функций, применяемых при терминальном подходе, не удается выразить в аналитической или алгоритмической форме, и именно поэтому приходится прибегать к целенаправленному подходу [5].

Для того чтобы сделать наше рассмотрение более полным, необходимо отмстить следующее.

a) Как правило, свойства, рассматриваемые в теории систем, относятся, скорее, к таким аспектам реально существующих явлений, как обработка информации и принятие решений, чем к физическим (или другим) законам per se. В этом смысле теория систем есть теория обработки информации и принятия решений.

b) Существует два направления, по которым может развиваться общая теория систем. Можно начинать с некоторого класса реально существующих проблем и двигаться дальше путем формализации их вербальных описаний. В этом случае, исходя из самого абстрактного, наименее ограниченного описания, вводят затем дополнительные структуры и рассматривают следствия, вытекающие из каждого нового допущения. Такой подход мы будем называть формализацией. Второй подход, который мы назовем генерализацией, начинает с двух определенных классов математических моделей и на основе обобщения приходит к более широкому классу, сохраняющему свойства и отношения исходных классов. В этой статье мы будем иметь дело с формализацией. Генерализация подвергалась исследованию, в частности, в связи с решением проблем объединения теории управления и теории автоматов (представленных в алгебраической, а не в логической форме) [6]; [7]; [15].

2. Ограниченности математической теории абстрактных систем

Прежде чем рассматривать потенциальную выгоду и полезность математической теории абстрактных систем, обратимся к ее недостаткам. Эту теорию можно критиковать с двух противоположных сторон.

1. Так как она является, по существу, математической теорией, в ней накладываются строгие ограничения на описание поведения реально существующих систем, особенно если дело касается сложных биологических или социальных явлений.
2. Так как эта теория пользуется довольно слабыми математическими структурами, с ее помощью невозможно решить серьезные проблемы или хотя бы даже получить достаточно полезные результаты.

Рассмотрим первое возражение. Несомненно, что теория систем не может быть шире, чем ее математические основания. Тем не менее, не исследовав более тщательно, что в действительности представляют собой эти основания, не следовало бы высказываться относительно возможностей этой теории. Подходящим исходным пунктом для такого рассмотрения может быть анализ понятия теории. Для наших целей наиболее приемлемо понятие теории, выдвинутое Г. Карри [8]. Для построения понятия теории берется класс (элементарных) высказываний P об исследуемом объекте. Необходимо отметить, что здесь речь идет об «интуитивно постигаемой совокупности элементов», которую Карри называет концептуальным классом. (Техническое различие между нашей точкой зрения и позицией, изложенной в [8], состоит в том, что у нас класс высказываний не обязательно должен быть определен.) Теория рассматривается как подкласс высказываний T ⊆ P которые принимаются за истинные. Оценка высказываний в качестве истинных может быть результатом экспериментов или следовать из некоторых постулатов относительно поведения наблюдаемых явлений. Для дальнейшего уточнения понятия теории нам необходимо выделить два аспекта теории: неформальный, касающийся смысла, интерпретации высказываний теории, и формальный, относящийся к структурным аспектам наблюдаемых явлений. Мы коснемся здесь только формального аспекта теории. Лингвистический анализ позволяет обнаружить два компонента высказываний: термы (имена), обозначающие рассматриваемые объекты, и функторы, обозначающие отношения между термами. В состав высказываний класса P входят некоторые неопределяемые конституенты, то есть такие, истинность или ложность которых не зависит от теории T, а определяется на содержательной основе исходя из содержания самих предложений. Значения неопределяемых элементов могут приниматься, вообще говоря, на базе некоторых концептуальных классов. Здесь мы примем допущение, что эти классы являются множествами в некоторой заданной аксиоматической теории множеств. Далее мы условимся, что имена будут обозначать определенные множества, а функторы — отношения.

Рассмотрим теперь математическую структуру, представляющую собой отношение на соответственным образом определенных множествах S ⊂ X₁ × ... × X_n Структуру S будем рассматривать как математическую модель теории T, если S есть общезначимая (valid) интерпретация T то есть если каждое высказывание из T истинно в S. Очевидно, для данной теории T существует большое число общезначимых математических моделей³. Отметим, что общезначимость требуется только относительно T. Поэтому некоторые модели могут быть некорректными в том смысле, что существуют высказывания, которые не входят в элементарную теорию T и ложны в содержательной интерпретации, тем не менее они истинны в S. Следовательно, модель может быть общезначимой, но некорректной в указанном смысле. Практически это случается очень часто, так как проверить заранее корректность данной модели нелегко (если вообще возможно). Общезначимая математическая модель S теории T и представляет собой абстрактную систему S, определение которой было дано в разделе 1; она является математической моделью реально существующей системы, относительно которой сформулирована теория T.

В итоге мы можем сказать, что если имеется некоторая теория, то можно ввести понятие системы. Ограничения, налагаемые общей теорией систем (как она определяется нами), следуют в основном из требования, чтобы область значений любого неопределяемого терма, входящего в высказывания теории, удовлетворяла аксиоматической теории множеств. По существу, это равносильно требованию, чтобы высказывания теории не содержали известных парадоксов (отнесения к самому себе и т. д.).

Проведенное рассуждение позволяет сформулировать важное утверждение: возможная неадекватность модели (системы) имеет место из-за ограниченностей нашей теории реально существующих явлений, а не из-за введения понятия системы. Если система мало структурирована и поэтому с ее помощью не удается получить многого, то это опять происходит скорее в результате недостаточности наших знаний о поведении реально существующей системы (то есть теории T), чем из-за применения формальных, математических методов.

Полный ответ на второе возражение, согласно которому математические структуры общей теории систем могут быть недостаточными для получения существенных результатов, можно дать только со временем. В принципе, конечно, такой ответ зависит от того, как определяется «полезность». Однако на нынешней стадии развития общей теории систем слишком рано предпринимать попытки подготовить исчерпывающую аргументацию против этого возражения. Если разработка общей теории систем необходима и неизбежна для дальнейшего понимания сложных явлений (а мне кажется, что так оно и есть), то, по всей видимости, наиболее разумно в данный момент сформулировать свои убеждения и оставить на будущее подготовку развернутого ответа на сформулированный вопрос. Тем не менее в работах [9]; [10]; [11] можно найти доводы, содержащие аргументацию против второго возражения.

3. Сложность и системы большого масштаба: абстрактный и иерархический подходы

Рассмотрим проблему сложности как в функционировании, так и в проектировании систем. В настоящее время, бесспорно, у нас еще нет определения понятия сложности; мы, вообще говоря, не думаем, что оно может быть разработано на формальной основе. Однако существует, по-видимому, согласие в том, что система считается «системой большого масштаба», или «сложной », если сочетание вычислительных, аналитических, экономических или любых других факторов не позволяет в достаточной мере достигнуть поставленных целей. Как можно подойти к анализу проблемы сложности? Традиционный путь состоял в использовании метода аппроксимаций. Однако существуют два новых подхода к этой проблеме, открывающие некоторые перспективы: 1) абстрактный подход; 2) иерархический, или многоуровневый подход.

1. При абстрактном подходе используется математическая модель, которая мало структирована и моделирует только некоторые доминирующие, «ключевые» особенности рассматриваемого явления. Предположим, например, что система описывается большим числом дифференциальных уравнений в частных производных. Изучение устойчивости такой системы по методу Ляпунова может оказаться очень сложным. Однако если удастся определить алгебраическую структуру преобразований этой системы, то проблему устойчивости можно исследовать алгебраически [12], используя в этом случае менее детализированное представление системы. Здесь математическая теория абстрактных систем может оказать большую помощь. Другие системные аспекты и свойства, например декомпозицию и структурирование систем, также можно изучать в рамках алгебры.

Следует отметить разницу между аппроксимацией и абстрактным подходом. В первом случае используется одна и та же математическая структура, а упрощение достигается путем элиминирования некоторых компонентов модели, которые рассматриваются как несущественные; например, дифференциальное уравнение пятого порядка заменяется уравнением второго порядка и анализируются только две «доминирующие»переменные состояния системы. При абстрактном подходе, напротив, используется иная математическая структура, более абстрактная, и система рассматривается как целое, но с менее детализированной точки зрения. Упрощение достигается не путем элиминирования переменных, а за счет того, что не рассматриваются некоторые детали, считающиеся несущественными.

2. При иерархическом подходе проблема расчленяется на ряд подпроблем, и каждая из них решается независимо от другой. Частные решения затем координируются на основе иерархии процессов решения, строящейся таким образом, чтобы как можно ближе подойти к полному решению всей проблемы. Декомпозиция и координация могут выполняться или во времени, или в пространстве. При разработке проблем проектирования и расчета систем подпроблемы рассматриваются последовательно во времени, а координация производится путем итерации. При разработке проблем сложных систем управления вся система расчленяется на подсистемы, действующие одновременно, а координация осуществляется путем «линейного» вмешательства в процесс реального функционирования подсистем.

Представляется интересным обратить внимание на то, что, несмотря на видимые различия между общей теорией систем и теорией многоуровневых (иерархических) систем, мотивация, лежащая в основе их разработки, очень сходна: изучение проблем сложных, крупномасштабных систем. Фактически обе эти теории следует рассматривать как направленные на изучение одного и того же типа проблем, но с различных исходных позиций.

4. Роль общей теории систем в технике

Математическая теория абстрактных систем может использоваться в технике в нескольких различных контекстах и для нескольких различных целей.

a) Сложность. Эта проблема прежде всего встает в связи с системами большого масштаба. К тому, что было сказано по этому поводу в разделе 3, сейчас нам достаточно добавить, что, по мере того как рассматриваемые проблемы становятся более сложными и все более широко осуществляется использование вычислительных машин для моделирования и решения этих проблем, все острее ощущается необходимость поисков концептуальной основы как их объяснения, так и решения.

b) Построение моделей и структурные представления. Один из самых важных шагов при проведении инженерной разработки — выбор структуры проектируемой системы или, иначе говоря, анализ структурных представлений поведения и деятельности системы. Для этой цели не подходит детальная математическая модель, даже если она имеется. По традиции для понимания полной композиции системы и ее последующих структурных представлений инженеры пользуются в основном блок-схемами. Главной привлекательной особенностью блок-схем является, конечно, их простота, а их основной недостаток— отсутствие точности. Общая теория систем может быть полезна как инструмент для построения основных структурных представлений системы, сохраняющих простоту блок-схем и в то же время удовлетворяющих всем требованиям математической точности. Действительную роль общей теории систем в инженерной методологии лучше всего, видимо, можно проиллюстрировать при помощи диаграммы, изображенной на рис. 1:

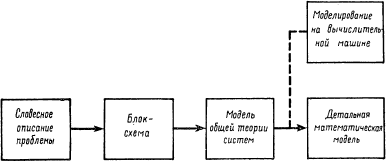
Рис. 1

Из диаграммы, в частности, следует, что модели общей теории систем находятся между представлениями систем с помощью блок-схем и детальными математическими (или вычислительными) моделями. Построение общесистемных моделей является необходимым особенно для анализа сложных систем, так как в этом случае разрыв между блок-схемой и детальной моделью может быть слишком велик. Наличие некоторых общесистемных методов, позволяющих решить ту или иную проблему (по крайней мере в предварительной форме) на уровне общей теории систем, свидетельствует о полезности введения этого этапа в процесс анализа и конструирования сложных систем.

c) Точное определение понятий и междисциплинарные связи. Общая теория систем создает основу для установления междисциплинарных связей, поскольку она является достаточно общей для того, чтобы не вводить своих специфических ограничений, и вместе с тем благодаря ее точности удается в значительной степени устранить неправильное понимание тех или иных проблем. Например, различные понятия адаптации, используемые в психологии, биологии, технике и т. д., можно сначала формализовать в терминах общей теории систем, а затем сопоставить друг с другом.

Часто заявляют, что теория систем должна отражать инвариантные аспекты различных реально существующих систем, справедливые для структурно сходных явлений из различных научных областей (дисциплин). Эту задачу можно выполнить только после того, как соответствующие понятия определены достаточно тщательно и точно — иначе слишком велика опасность путаницы. Сказанное позволяет рассматривать математическую теорию абстрактных систем как основу для формализации важнейших системных понятий. В этом смысле такая теория является базой «системного подхода» в целом и теории систем в частности. При использовании общей теории систем в этом контексте важно то обстоятельство, что после введения точного понятия решающей оказывается не «корректность» определения в какой-либо данной интерпретации, а скорее вопрос о том, определяется ли понятие таким образом, чтобы его можно было бы исследовать, сравнивать и затем изменять, если оно не удовлетворяет некоторым интуитивным требованиям. Другими словами, необходима база для объективной оценки формализации свойств реально существующих систем. В этом смысле общая теория систем предлагает «язык» для междисциплинарных связей. Такое употребление общей теории систем может показаться тривиальным с чисто математической точки зрения, но оно нетривиально с точки зрения управления инженерной разработкой большой системы, когда группа специалистов по различным дисциплинам работает над одной сложной проблемой.

5. Формализация понятия целенаправленности в общей теории систем

Как уже указывалось в разделе 1, понятие целенаправленности лежит в основании столь же (если не более) важного подхода к изучению реально существующих систем, как и терминальный подход. В этом разделе мы более точно определим в общесистемных терминах понятие целенаправленной системы с тем, чтобы проиллюстрировать и применяемый нами процесс формализации и тот тип понятий, который обычно используется в общей теории систем.

Если дана система

S ⊂ X × Y,

(1)

то, для того чтобы построить целенаправленное представление S, необходимо два предварительных понятия, а именно понятие цели и понятие принятия решения. (Для простоты будем рассматривать S как функцию, означающую, что элементы X являются парами вход — состояние.)

a) Цель

Пусть X ⊂ M × U. Тогда цель для S задается тройкой отношений α = (G, T, R), определяемых относительно множества V следующим образом:

G : S → V, T : U → V, R ⊂ V × V

(2)

Здесь V — множество значений или мер выполнения; G — функция выполнения (или целевая функция), которая каждому состоянию или проявлению системы s ∈ S приписывает значение G(s) ∈ V. Т — относительная функция допустимости (tolerance (reference) function). Для каждого u ∈ U, T определяет значение T(u) ∈ V, которое используется для оценки выполнения данного y = S(m, u). Наконец, R — отношение удовлетворительности (satisfaction relation). Для каждого (m, u) ∈ M ⊂ U удовлетворительность поведения системы оценивается относительно G(m, u), S(m, u), T(u) и R.

При данной цели α = (G, T, R) системы S мы имеем два понятия, связывающие входы с целью.

Вход x ∈ X достигает цели α, если

(G(x, S(x)), T(u)) ∈ R

(3)

где x = (m, u).

Вход m ∈ M удовлетворяет цели α относительно U' ⊂ U, если для всех u ∈ U' вход x = (m, u) достигает цели α, то есть для всех u ∈ U' имеет место

(G(m, u, S(m, u)), T(u)) ∈ R

(4)

Тройку β = (S, U', α) будем называть проблемой решения. Вход m ∈ M удовлетворяет проблеме решения (S, U', α), если он удовлетворяет цели α относительно U'.

b) Принятие решения (система принимающая решения)

Систему

S : M × U → M,

(5)

будем называть системой, принимающей решения, если проблема решения β определена так, что для каждого (m, u) ∈ M × U выход y = S(m, u) удовлетворяет β (в указанном смысле).

Более точно, будем называть систему S принимающей решения, если дано:

α) Пара отображений

P : Y × U → M, W : U → M,

(6)

таких, что

m = W(u) ↔ (S(m, u) = y) ∧ (P(y, u) = m),

(7)

то есть W есть композиция S и P, как это показано в работе [6].

β) Цель α для P такая, что для всех u ∈ U, S(ω, W(u)) удовлетворяет проблеме решения β = (P, U', α), где U' ⊂ U определяется через предварительно определенное многозначное отображение F : U → π(U).

Здесь U интерпретируется как множество неопределенностей (uncertaintly set), а отображение F используется для выбора (например, путем предсказания) подмножества U' для которого, выход системы S должен достигать данной цели.

c) Целенаправленная система

Теперь, наконец, мы в состоянии ввести понятие целенаправленной системы.

S : X → Y,

(8)

Для данной системы (8) существует два способа определения S как целенаправленной системы.

1. Пусть α является целью для S. Система считается целенаправленной системой (с разомкнутым контуром), если каждый x ∈ X удовлетворяет цели α.

2. S считается целенаправленной системой (с обратной связью), если дано множество M вместе с парой отображений (D, Р)

   P : M × X → Y, D : X × Y → M,

   (9)

   таких, что

   α) y = S(x) ↔ (P(m, x) = y) ∧ (D(x, y) = m).

   β) D принимает решения относительно цели α для отображения P_M, определенного на M × U, в Y, то есть:

   PM : M × U → Y.

   (10)

Очевидно, что, согласно второму понятию, S есть целенаправленная система, если дана пара отображений (P, D), таких, что S есть композиция (с обратной связью) Р и D и, кроме того, D принимает решение относительно цели α, определенной для P_M.

Исходя из понятия целенаправленной системы можно определить некоторые другие понятия, такие, как обучение (адаптация), самоорганизация и т. д. Например, обучение можно определить как процесс, направленный на уменьшение множества неопределенностей U [13]; [14], а самоорганизацию — как процесс изменения структуры целенаправленного процесса, то есть функций, определяющих целенаправленную систему (таких, как функция выполнения, модель процесса P_M, функция допустимости, отношение удовлетворительности и т. д.).

Литература

1. Mesarovic М. D., Foundations for a General Systems Theory, «Views on General Systems Theory», ed. by Mesarovic M. D., New York, John Wiley, 1964 (русский перевод — Месарович М., Основания общей теории систем, сб. «Общая теория систем», «Мир», 1966, стр. 15—48).
2. Mesarovic М. D., On the Auxiliary Functions and Constructive Specification of the General Time Systems, «Report Systems Research Center SRC 85-A-66-33», Case institute of Technology, Ohio 1966.
3. Windeknecht T. G., Mathematical Systems Theory: Causality, «Mathematical Systems Theory», Springer-Verlag, 1967.
4. Rasiоwа Н. and Siкоrsкi R., The Mathematics of Metamathematics, Warszawa, 1963.
5. Mesarovic M. D., Systems Theory and Biology — View of a Theoretician, «Systems Theory and Biology», Proceedings of the Third Systems Symposium at Case Institute of Technology, ed, by Mesarovic M. D., New York, Springer-Verlag, 1968.
6. Zadeh L., The Concept of State in Systems Theory, «Views on General Systems Theory», ed by Mesarovic M. D., New York, J. Wiley, 1964 (русский перевод — Заде Л., Понятие состояния в теории систем, «Общая теория систем», «Мир», 1966, стр. 49—65).
7. Каlmаn R., Algebraic Aspects of the Theory of Dynamical Systems, «Differential Equations and Dynamical Systems», Academic Press, 1967.
8. Curry H., Foundation of Mathematical Logic, New York, McGraw-Hill, 1963.
9. Windeknecht T. G., An Axiomatic Theory of Systems, «Proceedings 1967 Systems Science and Cybernetics Conference», Boston, Massachusetts, 1967.
10. Вirta L., The Concept of Generativity in General Systems Theory, «Procedings 1967 Systems Science and Cybernetics Conference», Boston, Massachusetts, 1967.
11. Macko D., Hierarchical and Multi-Level Systems, «Proceedings 1967 Systems Science and Cybernetics Conference», Boston, Massachusetts, 1967.
12. Windekneсht T. G., Mesarovic M. D., On General Dynamical Systems and Finite Stability, «Differential Equations and Dynamical Systems», Academic Press, 1967.
13. Mesarovic M. D., A Unified Theory of Learning and Information, «Proceedings of the 1st Computers and Information Science Symposium», Washington, Spartan Press, 1963.
14. Mesarovic M. D., Toward a Formal Theory of Problem Solving, «Symposium on Computer Augmentation of Human Reasoning», Washington, Spartan Press, 1965.
15. Wуmore W., Mathematical Theory of Systems Engineering, New York, J. Wiley, 1967.

Сноски

1. Термин «реально существующая система» используется здесь только как обозначение класса физических, экономических и т. д. (или даже концептуальных) взаимосвязанных объектов (или явлений), определенных в пределах данных областей исследования. По существу, он представляет собой интерпретацию определенных математических моделей, в частности модели, излагаемой в этой работе.
2. Следует отметить, что по установившемуся обычаю в математике термином «теория множеств» обозначают только дисциплину, изучающую отношения между множествами (и элементами множеств) с очень простой (если она вообще имеется) дополнительной структурой (таковы, например, упорядоченные множества). Специализированные области математики, в которых исследуются множества, имеющие большее число свойств, не считаются частью теории множеств. Например, если рассматриваемые множества обладают некоторыми функциями, отображающими элементы множества в само это множество, то говорят о (частных) алгебрах, а если на рассматриваемых множествах определены некоторые многозначные функции, то говорят о (общей) топологии, и т. д.
3. Необходимо отметить, что применительно к некоторым типам формализованных теорий (таким метаматематическим системам, как пропозициональное исчисление и т. д.) ведутся довольно активные исследования в области математической теории моделей (строятся модели этих частных формализованных теорий). Нас интересуют здесь, конечно, более широкие понятия теории и ее модели (поскольку теория не является просто индуктивным классом высказываний).

↑	Оглавление
←	Системы, организации и междисциплинарные исследования (Р. Л. Акоф)	Целое и развитие в свете кибернетики (О. Ланге)	→