«Введение в системный анализ и моделирование»

В. М. Казиев

↑	Оглавление
←	Глава 2.1, «Цель, задача, структура, система, системность»	Глава 2.3, «Мера сложности системы»	→

2.2 Классификация систем. Большие и сложные системы

Классификацию систем можно осуществить по разным критериям. Ее часто жестко невозможно проводить и она зависит от цели и ресурсов. Приведем основные способы классификации (возможны и другие критерии классификации систем).

1. По отношению системы к окружающей среде:
   • открытые (есть обмен с окружающей средой ресурсами);
   • закрытые (нет обмена ресурсами с окружающей средой).
2. По происхождению системы (элементов, связей, подсистем):
   • искусственные (орудия, механизмы, машины, автоматы, роботы и т.д.);
   • естественные (живые, неживые, экологические, социальные и т.д.);
   • виртуальные (воображаемые и, хотя они в действ ительности реально не существующие, но функционирующие так же, как и в случае, если бы они реально существовали);
   • смешанные (экономические, биотехнические, организационные и т.д.).
3. По описанию переменных системы:
   • с качественными переменными (имеющие только лишь содержательное описание);
   • с количественными переменными (имеющие дискретно или непрерывно описываемые количественным образом переменные);
   • смешанного (количественно — качественное) описания.
4. По типу описания закона (законов) функционирования системы:
   • типа «Черный ящик» (неизвестен полностью закон функционирования системы; известны только входные и выходные сообщения системы);
   • не параметризованные (закон не описан, описываем с помощью хотя бы неизвестных параметров, известны лишь некоторые априорные свойства закона);
   • параметризованные (закон известен с точностью до параметров и его возможно от ADE нести к некоторому классу зависимостей);
   • типа «Белый (прозрачный) ящик» (полностью известен закон).
5. По способу управления системой (в системе):
   • управляемые извне системы (без обратной связи, регулируемые, управляемые структурно, информационно или функционально);
   • управляемые изнутри (самоуправляемые или саморегулируемые — программно управляемые, регулируемые автоматически, адаптируемые — приспосабливаемые с помощью управляемых изменений состояний и самоорганизующиеся — изменяющие во времени и в пространстве свою структуру наиболее оптимально, упорядочивающие свою структуру под воздействием внутренних и внешних факторов);
   • с комбинированным управлением (автоматические, полуавтоматические, автоматизированные, организационные).

Под регулированием понимается коррекция управляющих параметров по наблюдениям за траекторией поведения системы — с целью возвращения системы в нужное состояние (на нужную траекторию поведения системы; при этом под траекторией системы понимается последовательность принимаемых при функционировании системы состояний системы, которые рассматриваются как некоторые точки во множестве состояний системы).

Пример. Рассмотрим экологическую систему «Озеро». Это открытая, естественного происхождения система, переменные которой можно описывать смешанным образом (количественно и качественно, в частности, температура водоема — количественно описываемая характеристика), структуру обитателей озера можно описать и качественно, и количественно, а красоту озера можно описать качественно. По типу описания закона функционирования системы, эту систему можно отнести к не параметризованным в целом, хотя возможно выделение подсистем различного типа, в частности, различного описания подсистемы «Водоросли», «Рыбы», «Впадающий ручей», »Вытекающий ручей», «Дно», «Берег» и др. Система «Компьютер» — открытая, искусственного происхождения, смешанного описания, параметризованная, управляемая извне (программно). Система «Логический диск» — открытая, виртуальная, количественного описания, типа «Белый ящик» (при этом содержимое диска мы в эту систему не включаем!), смешанного управления. Систем «Фирма» — открытая, смешанного происхождения (организационная) и описания, управляемая изнутри (адаптируемая, в частности, система).

Система называется большой, если ее исследование или моделирование затруднено из-за большой размерности, т.е. множество состояний системы S имеет большую размерность. Какую же размерность нужно считать большой? Об этом мы можем судить только для конкретной проблемы (системы), конкретной цели исследуемой проблемы и конкретных ресурсов.

Большая система сводится к системе меньшей размерности использованием более мощных вычислительных средств (или ресурсов) либо разбиением задачи на ряд задач меньшей размерности (если это возможно).

Пример. Это особенно актуально при разработке больших вычислительных систем, например, при разработке компьютеров с параллельной архитектурой или алгоритмов с параллельной структурой данных и с их параллельной обработкой.

Система называется сложной, если в ней не хватает ресурсов (главным образом, — информационных) для эффективного описания (состояний, законов функционирования) и управления системой — определения, описания управляющих параметров или для принятия решений в таких системах (в таких системах всегда должна быть подсистема принятия решения).

Пример. Сложными системами являются, например, химические реакции, если их рассматривать на молекулярном уровне; клетка биологического образования, рассматриваемая на метаболическом уровне; мозг человека, если его рассматривать с точки зрения выполняемых человеком интеллектуальных действий; экономика, рассматриваемая на макроуровне (т.е макроэкономика); человеческое общество — на политико-религиозно-культурном уровне; ЭВМ (особенно, — пятого поколения), если ее рассматривать как средство получения знаний; язык, — во многих аспектах.

Сложность этих систем обусловлена их сложным поведением. Сложность системы зависит от принятого уровня описания или изучения системы-макроскопического или микроскопического.

Сложность системы может быть внешней и внутренней.

Внутренняя сложность определяется сложностью множества внутренних состояний, потенциально оцениваемых по проявлениям системы, сложностью управления в системе.

Внешняя сложность определяется сложностью взаимоотношений с окружающей средой, сложностью управления системой потенциально оцениваемых по обратным связям системы и среды.

Сложные системы бывают:

• сложности структурной или статической (не хватает ресурсов для построения, описания, управления структурой);
• динамической или временной (не хватает ресурсов для описания динамики поведения системы и управления ее траекторией);
• информационной или информационно — логической, инфологической (не хватает ресурсов для информационного, информационно-логического описания системы);
• вычислительной или реализации, исследования (не хватает ресурсов для эффективного прогноза, расчетов параметров системы или их проведение затруднено нехваткой ресурсов);
• алгоритмической или конструктивной (не хватает ресурсов для описания алгоритма функционирования или управления системой, для функционального описания системы);
• развития или эволюции, самоорганизации (не хватает ресурсов для устойчивого развития, самоорганизации).

Чем сложнее рассматриваемая система, тем более разнообразные и более сложные внутренние информационные процессы приходится актуализировать для того, чтобы была достигнута цель системы, т.е. система функционировала или развивалась как система.

Пример. Поведение ряда различных реальных систем (например, соединенных между собой проводников с сопротивлениями x₁, x₂, ..., x_n или химических соединений с концентрациями x₁, x₂, ..., x_n участвующих в реакции химических реагентов) описывается системой линейных алгебраических уравнений, записываемых в матричном виде:

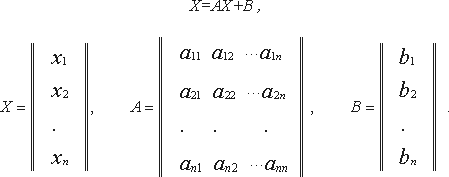
Заполненность матрицы А (ее структура, связность) будет отражать сложность описываемой системы. Если, например, матрица А — верхнетреугольная матрица (элемент, расположенный на пересечении i-ой строки и j-го столбца всегда равен 0 при i > j), то независимо от n (размерности системы) она легко исследуется на разрешимость. Для этого достаточно выполнить обратный ход метода Гаусса. Если же матрица А — общего вида (не является ни симметричной, ни ленточной, ни разреженной и т.д.), то систему сложнее исследовать (так как при этом необходимо выполнить более вычислительно и динамически сложную процедуру прямого хода метода Гаусса). Следовательно, система будет обладать структурной сложностью (которая уже может повлечь за собой и вычислительную сложность, например, при нахождении решения). Если число n достаточно в  елико, то неразрешимость задачи хранения матрицы А верхнетреугольного вида в оперативной памяти компьютера может стать причиной вычислительной и динамической сложности исходной задачи. Попытка использовать эти данные путем считывания с диска приведет к многократному увеличению времени счета (увеличит динамическую сложность — добавятся факторы работы с диском).

Пример. Пусть имеется динамическая система, поведение которой описывается задачей Коши вида:

y'(t) = k • y(t), y(0) = a

Эта задача имеет решение:

y = a • e−k•t

Отсюда видно, что y(t) при k = 10 изменяется на порядок быстрее, чем y(t) при k = 1 и динамику системы сложнее будет отслеживать: более точное предсказание для t → 0 и малых c связано с дополнительными затратами на вычисления т.е. алгоритмически, информационно, динамически и структурно «не очень сложная система» (при a, k ≠ 0) может стать вычислительно и, возможно, эволюционно сложной (при t → 0), а при больших t (t → ∞) и непредсказуемой. Например, при больших t значения накапливаемых погрешностей вычислений решения могут перекрыть значения самого решения. Если при этом задавать нулевые начальные данные а ≠ 0, то система может перестать быть, например, информационно несложной, особенно, если а трудно априорно определить.

Пример. Упрощение технических средств для работы в сетях, например, научные достижения, позволяющие подключать компьютер непосредственно к сети, «к розетке электрической сети» наблюдается наряду с усложнением самих сетей, например, увеличением количества абонентов и информационных потоков в Интернет. Наряду с усложнением самой сети Интернет упрощаются (для пользователя!) средства доступа к ней, увеличиваются ее вычислительные возможности.

Структурная сложность системы оказывает влияние на динамическую, вычислительную сложность. Изменение динамической сложности может привести к изменениям структурной сложности, хотя это не является обязательным условием. При этом сложной системой может быть и система, не являющаяся большой системой; существенным при этом может стать связность (сила связности) элементов и подсистем системы (см. вышеприведенный пример с матрицей системы линейных алгебраических уравнений).

Само понятие сложности системы не является чем-то универсальным, неименным и может меняться динамически, от состояния к состоянию. При этом и слабые связи, взаимоотношения подсистем могут повышать сложность системы.

Пример. Рассмотрим процедуру деления единичного отрезка [0; 1] с последующим выкидыванием среднего из трех отрезков и достраиванием на выкинутом отрезке равностороннего треугольника (рис.); эту процедуру будем повторять каждый раз вновь к каждому из остающихся после выкидывания отрезков. Этот процесс является структурно простым, но динамически является сложным, более того образуется динамически интересная и трудно прослеживаемая картина системы, становящейся «все больше и больше, все сложнее и сложнее». Такого рода структуры называются фракталами или фрактальными структурами (фрактал — от fraction — дробь и fracture — излом т.е. изломанный объект с дробной размерностью). Его отличительная черта — самоподобие, т.е. сколь угодно малая часть фрактала по своей структуре подобна целому, как ветка — дереву.

Рис. Фрактальный объект (кривая Коха)

Уменьшив сложность системы можно часто увеличить ее информативность, исследуемость.

Пример. Выбор рациональной проекции пространственного объекта делает чертеж более информативным. Используя в качестве устройства эксперимента микроскоп можно рассмотреть некоторые невидимые невооруженным глазом свойства объекта.

Система называется устойчивой, если она сохраняет тенденцию стремления к тому состоянию, которая наиболее соответствует целям системы, целям сохранения качества без изменения структуры или не приводящим к сильным изменениям структуры системы на некотором заданном множестве ресурсов (например, на временном интервале). Понятие «сильное изменение» каждый раз должно быть конкретизировано, детерминировано.

Пример. Рассмотрим маятник, подвешенный в некоторой точке и отклоняемый от положения равновесия на угол 0 ≤ φ ≤ π. Маятник будет структурно, вычислительно, алгоритмически и информационно устойчив в любой точке, а при φ = 0 (состояние покоя маятника) — устойчив и динамически, эволюционно (самоорганизационные процессы в маятнике на микроуровне мы не учитываем). При отклонении от устойчивого состояния равновесия маятник, самоорганизуясь, стремится к равновесию. При φ = π маятник переходит в динамически неустойчивое состояние. Если же рассматривать лед (как систему), то при температуре таяния эта система структурно неустойчива. Рынок — при неустойчивом спросе (предложении) неустойчив структурно, эволюционно.

Система называется связной, если любые две подсистемы обмениваются ресурсом, т.е. между ними есть некоторые ресурсоориентированные отношения, связи.

Лабораторная работа N2

↑	Оглавление
←	Глава 2.1, «Цель, задача, структура, система, системность»	Глава 2.3, «Мера сложности системы»	→