«Введение в системный анализ и моделирование»
В. М. Казиев
| ↑ | Оглавление | ||
| ← | Глава 2.2, «Классификация систем. Большие и сложные системы» | Глава 2.4, «Управление в системе и управление системой» | → |
2.3 Мера сложности системы
Почти во всех учебниках можно встретить словосочетания «сложная задача», «сложная проблема», «сложная система» и т.п. Интуитивно, как правило, под этими понятиями понимается какое-то особое поведение системы или процесса, делающее невозможным описание, исследование, предсказание поведения, развития системы. При определении меры сложности системы важно выделить инвариантные свойства систем или информационные инварианты и вводить меру сложности систем на основе их описаний.
Пусть μ(S) — мера сложности или функция (критерий, шкала) заданная (заданный) на некотором множестве элементов и подсистем системы S.
Как же определять меру сложности для систем различной структуры? Ответ на этот не менее сложный вопрос не может быть однозначным и даже часто определенным. Возможны различные способы определения сложности структуры систем. Сложность структуры, можно определять топологической энтропией — сложностью конфигурации структуры (системы): S = k • ln(W), где k = 1.38 • 10−16 (эрг/град) — постоянная Больцмана, W — вероятность состояния системы. В случае разной вероятности состояний эта формула будет иметь вид (мы ниже вернемся к детальному обсуждению этой формулы и ее различных модификаций):
| S = −k • ∑(pi • ln(pi)) |
Пример. Определим сложность иерархической системы как число уровней иерархии. Увеличение сложности при этом требует больших ресурсов для достижения цели. Определим сложность линейной структуры как количество подсистем системы. Определим сложность сетевой структуры как максимальную из сложностей всех линейных структур соответствующих различным стратегиям достижения цели (путей ведущих от начальной подсистемы к конечной). Сложность системы с матричной структурой можно определить количеством подсистем системы. Усложнение некоторой подсистемы системы приведет к усложнению всей системы в случае линейной структуры, возможно, — в случае иерархической, сетевой и матричной структур.
Пример. Для многоатомных молекул число межъядерных расстояний (оно определяет конфигурацию молекулы) можно считать оценкой сложности топологии (геометрической сложности) молекулы. Из химии и математики известна эта оценка: 3 • N − 6, где N — число атомов в молекуле. Для твердых растворов можно считать W равной числу перестановок местами атомов разных сортов в заданных позициях структуры; для чистого кристалла W = 1, для смешанного — W > 1. Для чистого кристалла сложность структуры S = 0, а для смешанного — S > 0, что и следовало ожидать.
Понятие сложности детализируется и конкретизируется в различных предметных областях по-разному. Для конкретизации этого понятия необходимо учитывать предысторию, внутреннюю структуру (сложность) системы и управления, приводящие систему к устойчивому состоянию. Впрочем все внутренние связи на практике достаточно трудно не только описать, но и обнаружить.
Пример. В эколого-экономических системах сложность системы может часто пониматься как эволюционируемость, сложность эволюции системы, в частности, мера сложности — как мера, функция изменений, происходящих в системе в результате контакта с окружающей средой и эта мера может опредляться сложностью взаимодействия между системой (организмом, организацией) и средой, ее управляемости. Эволюционную сложность эволюционирующей системы можно определить как разность между внутренней сложностью и внешней сложности (сложности полного управления системой). Решения в таких системах должны приниматься (для устойчивости систем) таким образом, чтобы эволюционная сложность равнялась нулю т.е. чтобы совпадали внутренняя и внешняя сложности. Чем меньше эта разность, тем устойчивее система, например, чем более сбалансировано внутрирыночные отношения и регулирующие их управляющие государственные воздействия — тем устойчивее рынок и рыночные отношения.
Пример. В математических, формальных системах сложность системы может пониматься как алгоритмизируемость, вычислимость оператора системы S, в частности, как число операции и операндов, необходимых для получения корректного результата при любом допустимом входном наборе.
Пример. Сложность программного комплекса L может быть определена как логическая сложность и измерена в виде:
| L = L1/L2 + L3 + L4 + L5 |
где L1 — общее число всех логических операторов, L2 — общее число всех исполняемых операторов, L3 — показатель сложности всех циклов (определяется с помощью числа циклов и их вложенности), L4 — показатель сложности циклов (он определяется числом условных операторов на каждом уровне вложенности), L5 — определяется числом ветвлений во всех условных операторах.
При исследовании сложности систем (явлений) полезно представлять (описывать) системы описанными выше симплициальными комплексами. Рассмотрим пример их использования при анализе и оценке сложности на базе примера, аналогичного примеру, приведенному в книге Дж. Касти [ ].
Пример. Рассматривается трагедия В. Шекспира «Ромео и Джульетта». Выделим и опишем 3 совокупности: А — пьеса, акты, сцены, мизансцены; В — действующие лица; С — комментарии, пьеса, сюжет, явление, реплики. Определим иерархические уровни и элементы этих совокупностей.
- А:
- уровень N+2, Пьеса;
- уровень N+1, Акты {a1, a2, a3, a4, a5};
- уровень N, Сцены {s1, s2, ..., sq};
- уровень N−1, Мизансцены {m1, m2, ..., m26}.
- В:
- все уровня N, Действующие лица {c1, c2, ..., c25} = {Ромео, Джульетта, ...}.
- С:
- уровень N+3, Пролог (адресованы непосредственно зрителю и лежат вне действий разворачивающихся в пьесе);
- уровень N+2, Пьеса;
- уровень N+1, Сюжетные линии {p1, p2, p3, p4} = {Вражда семейств Капулетти и Монтекки в Вероне, Любовь Джульетты и Ромео и их венчание, Убийство Тибальда и вражда семейств требует отмщения, Ромео вынужден скрываться, Сватание Париса к Джульетте, Трагический исход};
- уровень N, Явления {u1, u2, ..., u8} = {Любовь Ромео и Джульетты, Взаимоотношения между семейством Капулетти и Монтекки, Венчание Ромео и Джульетты, Схватка Ромео и Тибальда, Ромео вынужден скрываться, Сватовство Париса, Решение Джульетты, Гибель влюбленных};
- уровень N−1, Реплики {r1, r2, ..., r104}={104 реплики в пьесе, которые определяются как слова, обращенные к зрителю, действующему лицу и развивающие неизвестный пока зрителю сюжет}.
Отношения, связи между этими совокупностями на различных уровнях иерархии определяемы из этих совокупностей. Например, если Y — сюжеты, X — действующие лица, то естественно определить связь λ между X,Y так: действующее лицо из совокупности X уровня N+1 участвует в сюжете Y уровня N+1. Тогда связность структуры трагедии можно изобразить схемой вида:
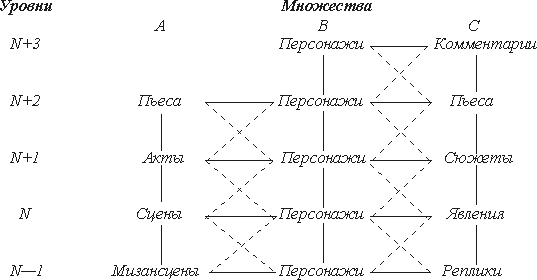
Рис. Схема структурных связей пьесы
В этом комплексе K(Y,X) все три сюжета становятся отдельными компонентами только на уровне связности q = 8. Это означает, что сюжетные линии могут быть различны только зрителями, следящими за 9 действующими лицами. Аналогично, при q = 6 имеются всего 2 компоненты {p1, p2}, {p3}. Следовательно, если зрители могут отслеживать только 7 персонажей, то они видят пьесу, как бы состоящую из двух сюжетов, где p1, p2 (мир влюбленных и вражда семейств) объединены. В комплексе K(Y, X) при q = 5 имеются 3 компоненты. Следовательно, зрители видевшие только 6 сцен воспринимают 3 сюжета, не связанные друг с другом. Сюжеты р1 и р2 объединяются при q = 4 и поэтому зрители могут видеть эти два сюжета как один, если следят только за 5 сценами. Все 3 сюжета сливаются, когда зрители следят лишь за 3 сценами. В комплексе K(Y,X) явление u8 доминирует структуру при q = 35, u3 — при q = 26, u6 — при q = 10. Следовательно, u8 вероятнее всего поймут те зрители, которые прослушали 36 реплик, хотя для понимания u3 необходимо 27 реплик, а для понимания u6 — только 11 реплик. Таким образом, проведенный анализ дает понимание сложности системы.
| ↑ | Оглавление | ||
| ← | Глава 2.2, «Классификация систем. Большие и сложные системы» | Глава 2.4, «Управление в системе и управление системой» | → |