«Системный анализ и проектирование»
Е. Н. Живицкая
| ↑ | Оглавление | ||
| ← | Лекция 6, «Основные системно-теоретические задачи» | Лекция 8, «Основные положения теории систем» (2 часть) | → |
Лекция 7: Основные положения теории систем (1 часть)
Глобальные свойства системы
В настоящее время существенно увеличилось число проблем, решение которых не может быть получено редукционистскими методами, что, в свою очередь, возродило интерес к изучению и развитию холистских (или глобальных) подходов. В этой связи наша цель состоит в том, чтобы каталогизировать некоторые наиболее перспективные направления, включая вопросы связности, сложности и устойчивости. Для иллюстрации фундаментального различия между локальным и глобальным описанием системы рассмотрим простой пример — математический маятник
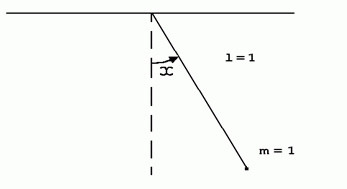
Рис.7.1 — Математический маятник
Если отклонение маятника от вертикали обозначим через x(t), то в локальной окрестности любого такого положения можно записать динамические уравнения движения
d2x/dt2 + sin(x) = 0, x(0) = x0, x(0) = 0,
в безразмерных единицах. Это уравнение описывает локальное поведение маятника в (бесконечно малой) окрестности положения 2 0x(t). Редукционист попытался бы «склеить» подобные локальные описания для последовательных точек в надежде достичь понимания глобального поведения. Хотя иногда такой подход оказывается успешным, непредвиденные проблемы, возникающие при его использовании, существенно снижают его эффективность.
Холист, приступая к решению этой же задачи, прежде всего заметил бы, что должны соблюдаться определенные глобальные свойства системы, и поэтому любое локальное поведение должно удовлетворять ограничениям, налагаемым глобальными свойствами. Если к тому же эти ограничения достаточно жестки, то можно ожидать, что любые локальные движения ими определяются однозначно.
В случае движения маятника эти глобальные ограничения определяются принципом Гамильтона-Якоби, согласно которому, глобальное движение системы соответствует минимуму полной энергии системы. Вводя гамильтониан
Н = Кинетическая энергия + Потенциальная энергия
видим, что движение системы должно быть таким, что гамильтониан
H(x, dx/dt) = (0,5) ⋅ (dx/dt)2 + 1 - cos(x)
достигает минимума. Это уравнение, очевидно, может быть сведено к уравнению движения, приведенному выше, т.е. локальные уравнения движения могут быть получены как следствие глобального принципа, а не выведены на основе рассуждений локального характера и использования второго закона Ньютона. С концептуальной точки зрения такое различие является фундаментальным.
Для систем, рассматриваемых в социально-экономических приложениях, не существует подобных общих законов (по крайней мере сейчас), и мы вынуждены ограничиться рассмотрением ряда глобальных свойств и методов работы с ними, рассчитывая на то, что освещение различных аспектов задачи поможет понять ее структуру в целом.
В качестве примера использования глобального подхода для решения системных задач рассмотрим ситуацию с заторами на транспортной магистрали. Учитывая наличие множества факторов, влияющих на дорожную ситуацию, можно попытаться склеить локальные ситуации, полученные методом Монте-Карло или методами теории очередей и т.д. Такой подход позволяет выявить множество деталей, однако в большинстве случаев остается неясным, как можно использовать полученные результаты для анализа других дорожных ситуаций. Холист в этом случае прибегнул бы к помощи статистической физики и попытался бы описать подобную ситуацию одним уравнением, пренебрегая дистанцией между машинами, причинами заторов и т.д. Главным для него было бы значение параметра q — плотности потока машин (число машин в час на километр пути). Время TA (минуты), необходимые для преодоления 1 км дороги, можно представить как сумму двух слагаемых
TA = TA0 + k ⋅ nA,
где TA0 — время, необходимое для преодоления участка дороги длиной А = 0 без учета помех со стороны других машин (q = 0) (TA0 = 0,5 мин/км соответствует скорости свободного движения 120 км/час); k ⋅ nA — дополнительное время, необходимое для преодоления участка А = 1 км, пропорциональное числу машин nA, находящихся на участке А в течение времени TA (т.е. задержка в условиях заторов является линейной функцией числа торможений и ускорений, или числа nA машин, участвующих в движении). Число nA — является произведением плотности потока машин (транспорта) q и длительности периода времени TA:
nA = q ⋅ TA / 60.
Учитывая предыдущие соотношения, получаем
TA = TA0 / (1 - k ⋅ q / 60)
Функция TA = f(q) является выпуклой: каждая дополнительная машина, приводящая к росту q, не только задерживается на участке А, но и является причиной задержки других машин. При значениях TA = 0,5 и k = 0,0266 имеется хорошее согласие между кривой и экспериментальными данными (рис.2.4)
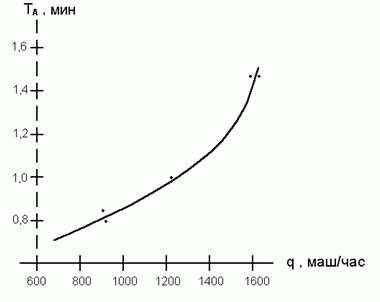
Рис.7.2 — Задержки, вызванные транспортными заторами
Полученное уравнение дает значение для q, лежащие гораздо ниже теоретического значения плотности q = 2,255 маш/час, соответствующей «параличу дороги». Таким образом, глобальный (а не локальный) подход позволяет построить содержательную модель временных задержек в транспортной магистрали с заторами.
Связность и графы
Структурная связность системы является, по-видимому, наиболее существенной ее качественной характеристикой. Кажется очевидным, что с исчезновением структурной связности исчезнет и сама система, поскольку само понятие системы подразумевает наличие «чего-то», находящегося в некотором отношении (или как-то связанного) с «чем-то».
Анализ задачи построения математического описания связности может быть осуществлен с помощью различных подходов, причем наиболее удачные из них построены на использовании теории графов и алгебраической (комбинаторной) топологии. Это является вполне закономерным, поскольку вопрос о характере связности «простейших элементов» единого целого интересует алгебру в гораздо большей степени, чем любую другую математическую дисциплину.
Сущность исследования связности состоит в том, чтобы осознать и уяснить себе те математические конструкции, которые описывают характер связи между отдельными компонентами системы. Если вообразить некоторую систему, в которой можно выделить n различных компонент (подсистем), то можно попытаться изобразить структуру (связную) графом (см.рис.2.5): n вершин изображают n подсистем системы, а дуга, соединяющая подсистемы i и j, показывает, что эти две подсистемы находятся в некотором отношении или как-то связаны между собой. Например, j-я подсистема может генерировать входы для i-й подсистемы, а i-я управлять j-й и т.д. Эту схему, естественно, можно развить. Так, например, можно ввести ориентацию на дугах и образовать ориентированный граф (орграф). Такое представление системы позволит изучать ситуации, когда i-я система влияет на j-ю, но не наоборот. Кроме того, можно учесть силу связности, сопоставив каждой направленной дуге некоторое число и т.д. Все это в конечном счете позволяет определить, какие компоненты системы влияют на другие компоненты и в какой степени. По существу теоретико-графовые модели позволяют несколько лучше понять, как можно было бы осуществить декомпозицию системы на меньшие составляющие без потери тех основных свойств, в силу которых она и является системой.
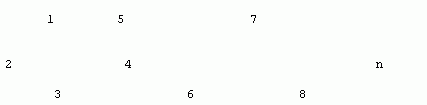
Рис.7.3 — Теоретико-графовое описание
Пример
Трофические структуры и экологические ниши. Рассмотрим экологическую структуру, состоящую из пяти видов: птиц, насекомых...

Рис.7.4 — Орграф простой системы
Трофическая структура этого сообщества изображается орграфом, вершины которого соответствуют видам. Дуга, проведенная от i-го вида к j-му, означает, что j-й вид является жертвой i-го вида. По данному графу можно построить матрицу смежности аналогичную матрице инциденций в теоретико-множественном описании, а также ряд других показателей, характеризующих важные аспекты системы.
| I \ j | Птицы | Лисы | Насекомые | Травы | Антилопы |
|---|---|---|---|---|---|
| Птицы | 0 | 0 | 1 | 1 | 0 |
| Лисы | 1 | 0 | 1 | 0 | 0 |
| Насекомые | 0 | 0 | 0 | 1 | 0 |
| Травы | 0 | 0 | 0 | 0 | 0 |
| Антилопы | 0 | 0 | 0 | 1 | 0 |
Отметим, что некоторые из компонент (например, травы) кажутся более важными для системы в целом, чем другие (например, птицы), и, по-видимому, это связано с такими экологическими понятиями, как трофический уровень и борьба видов. Важно подчеркнуть, что теоретико-графовое описание позволяет непосредственно увидеть некоторые геометрические свойства матрицы смежности.
Как бы ни были важны и удобны теоретико-графовые методы для зрительного анализа связности, их использование неизбежно связано с трудностями геометрического и аналитического характера, если учитывается структура самих компонент. Из общих соображений можно ожидать, что при попытке описать многомерную структуру планарным графом или, более общо, графом, изображенным на плоскости (это не одно и то же!), многое из геометрической структуры системы будет утеряно или в лучшем случае скрыто. По этой причине обратимся к другому возможному способу анализа связности, основанному на топологических идеях.
Связность и симплициальные комплексы
Приближенно симплициальный комплекс состоит из множества вершин X и множества симплексов Y, образованных из этих вершин в соответствии с заданным бинарным отношением.Симплициальный комплекс образован множеством симплексов Y, связанных через общие грани, т.е. через общие вершины. Например, можно положить Y = X = {птицы, лисы, насекомые, травы, антилопы}. При этом отношение таково: симплекс состоит из всех вершин, таких, что Xj является жертвой Yi. Таким образом, Yi = «птицы» — 1-симплекс, состоящий из вершин «насекомые» и «травы», y2 = «лисы» — 1-симплекс, состоящий из вершин «птицы» и «насекомые» и т.д. Отметим, что n-симплекс состоит из n+1 вершин и его размер на единицу меньше числа вершин.
Вообще говоря, p — симплекс представляется выпуклым многогранником с вершинами в эвклидовом пространстве, а комплекс Ky(X,L) совокупностью таких многогранников в эвклидовом пространстве E. Хотя размерность наверняка не превышает суммы размерностей всех симплексов из Ky(X,L), однако поскольку многие симплексы имеют общие грани, то размерность на самом деле окажется меньше. В действительности можно показать, что если dim[Ky(X,L)] = n, то 7 a 1 = 2⋅n + 1. Так, если dim[Ky(X,L)] = 1, то наибольший порядок есть p = 1, поэтому можно ожидать, что трехмерного пространства E3 будет достаточно, чтобы геометрически представить произвольный комплекс размерности 1. Это можно проиллюстрировать следующим образом: на плоскости (E2) надо соединить непересекающимися линиями три дома H1, H2 и H3 с источником газа, воды и электроэнергии. Неразрешимость поставленной задачи иллюстрирует наше утверждение. Задача графически изображена на рис.7.5, а ее решение в E3 показано на рис.7.6.
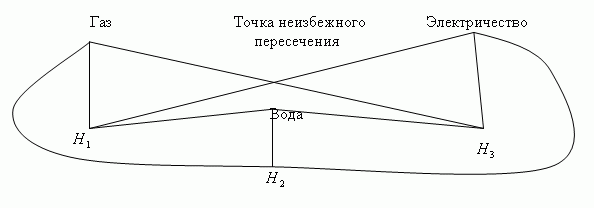
Рис.7.5 — Проблема пересечений в E2
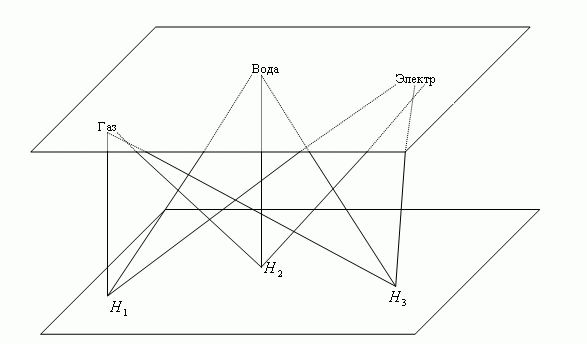
Рис.7.6 — Решение проблемы пересечений в E2
Основываясь на геометрической интуиции, можно изучать многомерную связную структуру комплекса Ky(X,L) различными способами с привлечением алгебраических методов. В связи с этим рассмотрим некоторые важные понятия.
q — связность
Это понятие связано с изучением цепочек связи, таких, что каждый симплекс в цепи имеет общую вершину с соседними симплексами, q = 0, 1, 2, ..., dim[К-1]. Геометрически эти цепи содержат достаточно много локальной информации относительно того, каким образом симплексы, составляющие комплекс, связаны друг с другом. Если представить себе,что мы можем «видеть» только в пространстве размерности 7. 0 q (скажем с помощью специальных очков), то, рассматривая комплекс Ky(X,L) мы увидим, что он распадается на несколько несвязанных элементов. Подобное геометрическое представление порождает алгебраическую теорию q-связности, позволяющую гораздо лучше понять процессы обмена информацией внутри комплекса.
Эксцентриситет
Для того, чтобы понять каким образом отдельные симплексы «вложены» в комплекс, вводится понятие эксцентриситета. Это понятие отражает как относительную важность данного симплекса для комплекса в целом (через его размерность), так и его значимость как связующего звена (через максимальное число его вершин, принадлежащих также любому другому симплексу). Другими словами, эксцентриситет позволяет увидеть и оценить, насколько «плотно» каждый симплекс вложен в комплекс.
Образ
Как мы уже отмечали в предыдущих лекциях для описания динамики системы необходимо ввести отображение каждого симплекса из Ky(X,L) П: Gi->k i = 0, 1 ... dim[K] r = 1, 2... card[K] в соответствующее числовое поле: Образ П отражает динамические изменения, происходящие в комплексе со временем. Поскольку каждый симплекс 7 s 4i 0 обладает характеристической геометрической размерностью, то же справедливо и для связанных с ним численных величин. Следует иметь в виду, что геометрическая структура налагает различные ограничения на изменение образа, т.е. на динамику системы.
Гомотопия
Вопрос о том, насколько «близким» является данный симплекс (цепь) к другому симплексу (цепи), представляет как теоретический, так и прикладной интерес. Если ввести понятие 1 гомотопия 0, то можно получить ответ не только на этот вопрос, но и на вопрос о том, можно ли непрерывным преобразованием трансформировать одну цепь в другую, не нарушая геометрии системы. Так, например, кривые А и A* на торе (см.рис.2.9) являются гомотопными, а кривые В и B* нет, поскольку наличие «дырки» в центре не позволяет непрерывно деформировать В в B*. Аналогичные понятия могут быть введены и для комплекса и не исключено, что они могут быть полезными при анализе его структуры. Хотя с чисто математической точки зрения изложенные геометрические понятия совершенно элементарны, они все же дают весьма подробную информацию, необходимую для понимания статической геометрии данного бинарного отношения и возможной динамики соответствующей ему связной структуры.
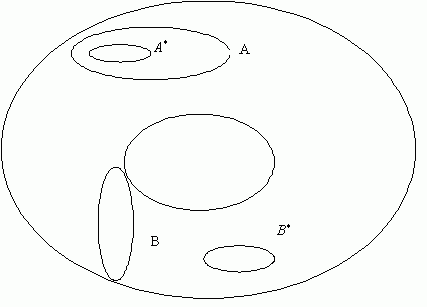
Рис.7.7 — Гомотопия на торе
| ↑ | Оглавление | ||
| ← | Лекция 6, «Основные системно-теоретические задачи» | Лекция 8, «Основные положения теории систем» (2 часть) | → |