«Системный анализ и проектирование»

Е. Н. Живицкая

↑	Оглавление
←	Лекция 7, «Основные положения теории систем» (1 часть)	Лекция 9, «Сигналы в системах»	→

Лекция 8: Основные положения теории систем (2 часть)

Сложность

Нет сомнения, что наиболее употребительным прилагательным в литературе по системному анализу является «сложный». Оно же является и наименее четко определенным. Чисто интуитивно мы ощущаем, что сложная система — это такая система, статическая структура или динамическое поведение которой «непредсказуемы», «запутаны», противоречат «здравому смыслу» и т.п. Короче говоря, сложная система — это нечто весьма сложное (одна из тавтологий системного анализа). Тем не менее, решение проблем, возникающих в вычислительной технике и теории алгоритмов, требовало разработки способов количественного описания этого понятия, и в результате целый ряд исследователей вынуждены были вплотную заняться вопросами сложности.

В основном сложность связана с двумя важными свойствами системы:

• математической структурой неприводимых компонент (подсистем) и
• способом, которым эти компоненты связаны между собой.

Отсюда с очевидностью следует, что сложность присуща самой системе, а тот факт, что сложность все же связана с отношением между наблюдателем и наблюдаемым объектом, при такой трактовке затушевывается и отступает на второй план. Однако, поскольку наш курс лекций носит в большей степени вводный характер, мы не будем затрагивать подобных релятивистских аспектов.

Первое свойство системы допускает возможность снижения видимой сложности системы путем объединения отдельных переменных в подсистемы. Это, например, имеет место в блок-схеме радиоприемника, где различные элементы системы (сопротивления, транзисторы и т.д.) сгруппированы в функциональные блоки, такие как цепь настройки или блок питания. Естественно, при такой декомпозиции преследуется цель позволить исследователю упростить анализ системы, рассматривая ее как слабо связанную совокупность взаимодействующих подсистем. Следует, однако, отметить, что хотя и предполагается, что взаимодействия между подсистемами будут слабыми, из этого вовсе не следует, что они действительно окажутся пренебрежимо малыми.

Второе свойство в значительной степени отражает сущность уже обсуждавшегося понятия связности и включает такие характеристики системы, как размерность, иерархия, длина цепей связи и т.п. Кроме того, очевидно, что вопросы, касающиеся динамического поведения системы, тесно связаны как со структурой отдельных элементов, так и со способом их организации.

Одним из важных аспектов понятия сложности является ее двоякая природа. Следует различать 1 структурную, или статическую 0 сложность, включающую связность и структуру подсистем, и 1 динамическую сложность 0, связанную с поведением системы во времени. Тот факт, что эти свойства могут быть сравнительно независимыми, можно проиллюстрировать на простых примерах. Так, например, обычные часы обладают высокой степенью статической сложности, однако их динамическая сложность, по существу, равна нулю, если, конечно, часы исправны. Напротив, поведение нелинейного осциллятора, описываемого уравнением Ван дер Поля,

x'' + λ ⋅ (x² - 1) + x = 0,

может быть весьма сложным в зависимости от параметра лямбда, и именно из-за этого «сложного» поведения он представляет теоретический и прикладной интерес. Со структурной же точки зрения осциллятор Ван дер Поля вовсе не является сложной системой.

Для иллюстрации непредсказуемого поведения, по-видимому, характерного для сложных систем, рассмотрим идеализированный линейный процесс, изображенный на рис.8.1. Это чисто условный пример, поэтому и его»содержательная» интерпретация также условна.

Предположим, что гипотетическая экономическая система включает два предприятия: механическую мастерскую и электростанцию, для которых требуются рабочие двух специальностей: механики и электрики. Оба предприятия имеют фиксированное количество рабочих мест и стремятся работать с полной занятостью. Смена персонала происходит достаточно быстро, так что полное число занятых рабочих равно ежегодному выпуску училищ. Всего имеется три училища: два небольших частных училища (механиков и электриков) и одно крупное общественное училище, готовящее равное число тех и других. Общественное училище готовит двух рабочих за «один доллар». Частные училища готовят одного рабочего на одно вакантное рабочее место, но так как частные училища более требовательны к абитуриентам, производительность труда их выпускников вдвое выше, чем у выпускников общественного училища, т.е., работающие предприятия отдают предпочтение таким выпускникам. Поскольку правительство субсидирует данные предприятия, они принимают на работу всех, оканчивающих общественное училище. Данная ситуация описывается следующими уравнениями:

M = D_m + G^S
P = D_m + G + D_e
E = G^s + D_e

где М — число механиков, Е — число электриков, Р — полные производительные силы (в терминах производительности труда выпускников частных училищ), D_m — спрос на механиков, D_e — спрос на электриков, G^s — ежегодный выпуск общественных училищ.

Отметим, что масштабирование уравнений несущественно, поскольку явления, которые мы сейчас опишем, не зависят от выбранного масштаба.

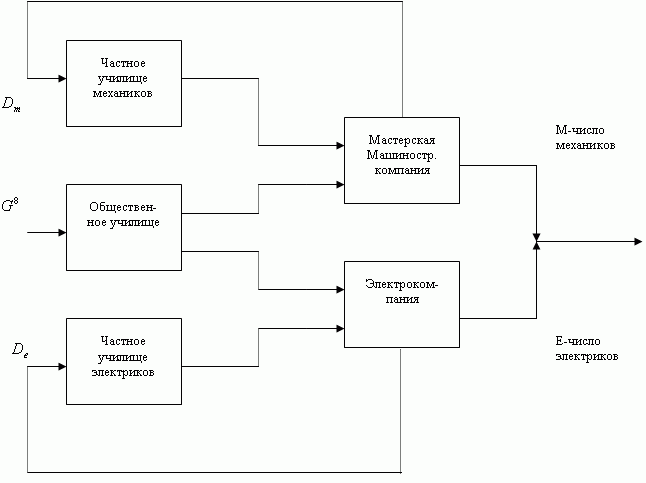
Рис.8.1 — Упрощенная блок-схема экономики развивающейся страны

где Р — полные производительные силы, G — ежегодный выпуск общественных училищ.

Предположим, что существует возможность управлять числом механиков и электриков и производительными силами. При этом управляющими органами являются оба предприятия и правительство. Правительство управляет переменной Р, изменяя G, мастерская управляет М через D_m, и электростанция контролирует Е, варьируя D_e.

В описанной ситуации возможно следующее парадоксальное поведение. Предположим, что на обоих предприятиях была полная занятость. Пусть правительство увеличивает G на единицу. Тогда предприятия в свою очередь уменьшают D_e и D_m на единицу, чтобы избежать превышения допустимой численности рабочих. Таким образом, изменение D_e и D_m приводит к уменьшению Р на две единицы. Итак, увеличение G на единицу приводит к уменьшению Р на две единицы. Этот вывод не зависит от деталей реализации стратегий управления и определяется лишь структурой управления и целей.

Парадокс исчезает, если правительство может регулировать D_m и D_e, а не только G. Однако основная проблема возникает из-за влияния других управляющих воздействий на взаимосвязь между управляемыми (М, Р, Е) и управляющими (D_m, G, D_e) переменными.

Вывод, который можно сделать из анализа этого примера, состоит в том, что, казалось бы, даже

в элементарных системах могут возникать совершенно неожиданные явления, если сложность взаимосвязей не изучена должным образом. Другой важный вывод состоит в том, что в отличие от обычных представлений такое парадоксальное поведение вызвано вовсе не наличием нелинейности, стохастических эффектов и т.п., а порождается исключительно структурой системы, имеющимися связями и ограничениями, присущими компонентам системы.

Данный пример иллюстрирует еще один важный момент, присущий понятию сложности системы, а именно различие между сложностью неуправляемой системы и сложностью управляемой системы. Грубо говоря, сложность неуправляемой системы определяется совокупностью статической и динамической сложности в отсутствие управления, или, более общо, процессом преобразования, при котором полностью используется потенциал системы. Процесс преобразования, однако, может привести к возникновению неустойчивых конфигураций. Так, например, неустойчивые конфигурации могут возникнуть из-за разрыва между вычислительными потребностями системы в целом и вычислительными возможностями составляющих ее подсистем.

Под сложностью управляемой системы понимается тот уровень сложности, который сопряжен с вычислениями, необходимыми для того, чтобы система была полностью управляемой. В данном случае неустойчивые конфигурации могут появиться, если быстродействие некоторых подсистем недостаточно велико, чтобы вовремя реагировать на изменения входных воздействий.

Связь между этими двумя типами сложности называют «эволюционной» сложностью 0, и говорят, что система полностью сбалансирована, когда ее потенциальные возможности используются полностью, т.е. когда сложность неуправляемой и управляемой системы одинакова.

Пример

Генетическая модель Джекоба-Моно. Предположим, что функции клетки клетки можно разделить на две группы: Обмен веществ М и генетическое управление G. Механизм работы клетки можно попытаться описать следующим образом. G пытается регулировать М, воспринимая выходы М и генерируя корректирующие входы для М (обычная обратная связь в теории регулирования). Если G осуществляет свое воздействие сообразно со сложностью неуправляемой системы, то возникают устойчивые конфигурации и оба типа сложности совпадают. В противном же случае, т.е. когда воздействия G слишком слабы или чрезмерно велики, могут возникнуть различные нарушения.

В целом можно сказать, что сложность — многозначное понятие, включающее как статические и динамические аспекты, так и элементы, связанные с управлением. Статическая сложность, по существу, связана со сложностью подсистем, составляющих данную систему, а динамическая включает вычислительные машины или микропроцессорные элементы, что объясняется необходимостью выработки сигналов управления при наличие взаимосвязности подсистем. Наконец, сложность управляемых систем, по существу, является мерой вычислительных возможностей, необходимых для реализации заданного поведения. В идеале математическая теория сложности должна достигнуть уровня, аналогичного уровню развития теории вероятностей. В то время как вероятность можно рассматривать как меру неопределенности в данной ситуации, сложность можно трактовать как меру понимания поведения системы.

Устойчивость

Наши системно-теоретические построения «покоятся» на трех китах: связность, сложность и устойчивость. Важность первых двух для понимания структуры системы была продемонстрирована нами достаточно наглядно. Что же касается устойчивости (или динамического поведения системы), то она практически еще не рассматривалась. Этот пробел можно восполнить, используя разнообразные понятия теории устойчивости.

К сожалению, термин «устойчивость» в высшей степени многозначен в литературе по системному анализу, будучи в постоянном употреблении для обозначения чего угодно, начиная с классической устойчивости по Ляпунову и кончая организационной жесткостью. Для всех возможных употреблений этого термина единственно общим моментом является интуитивное понимание того, что слово «устойчивый» обозначает, что нечто (может быть, система) способно реагировать на изменения в окружающей среде (например, возмущения, случайные помехи) и по-прежнему сохранять приблизительно то же самое поведение на протяжении определенного (возможно, бесконечного) периода времени. Совершенно ясно, что со столь нечетким и туманным «определением» устойчивости всякие попытки математического анализа устойчивости заведомо безнадежны. Тем не менее, такое «определение» создает некоторую интуитивную основу для более точных определений.

Для большей ясности изложения удобно ввести две категории понятия устойчивости. Первую из них назовем «классической» и будем использовать ее для обозначения задач исследования результатов внешних воздействий на фиксированные системы, т.е. таких задач, когда изменяется только окружающая среда, но не сама система. В качестве простого примера подобной ситуации рассмотрим классический маятник (см.рис.8.2).

Задача формулируется следующим образом: если сместить маятник из положения равновесия (A = 0) на некоторый угол, то может ли маятник вновь вернуться в положение = 0 за достаточно долгое, возможно бесконечное время? Как из физических, так и из математических соображений, очевидно, что так оно и будет для всех возмущений .

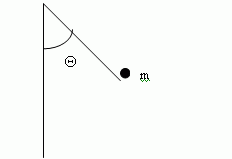
Рис.8.2 — Математический маятник

Таким образом, A = 0 является положением устойчивого равновесия (по Ляпунову). Положение A = 180 есть положение неустойчивого равновесия, поскольку сколь угодно малое отклонение от него в коне концов приведет систему в положение устойчивого равновесия.

Важно отметить, что величина начального смещения не влияет на динамику системы. Таким образом, налицо классическая ситуация, когда изменяется не структура системы, а лишь внешняя среда.

Классическая теория устойчивости в основном изучает равновесные состояния систем и динамику их поведения в малой окрестности этих состояний. Для исследования таких задач разработаны весьма совершенные методы. Подобные классические представления об устойчивости оказываются весьма плодотворными в физических и технических приложениях. Что касается их применения к анализу систем, изучаемых биологией, экономикой и общественными науками, то оно должно быть тщательно продумано и обосновано. Дело в том, что обычный режим функционирования подобных систем, как правило, далек от равновесного, и, кроме того, внешние воздействия постоянно изменяют само равновесное состояние. Короче говоря, постоянные времени таких систем настолько велики, что во многих случаях ценность классического анализа устойчивости практически незаметна.

В отличие от классического равновесного подхода, центральным элементом современных взглядов на вопросы устойчивости является понятие «структурной устойчивости». Здесь основной задачей является выявление качественных изменений в траектории движения при и изменениях структуры самой системы. Таким образом, здесь изучается поведение данной системы по отношению к поведению всех «близких» к ней аналогичных систем. Если рассматриваемая система ведет себя «почти так же», как и «соседние», то говорят, что она «структурно устойчива»; в противном случае — «структурно неустойчива». Для уточнения этого понятия необходимо четко определить, что такое «близкая» система, каков класс допустимых возмущений и что значит «схожесть поведения». Тем не менее, основная идея остается прозрачной, достаточно малые изменения структурно устойчивой системы должны приводить к соответственно малым изменениям ее поведения.

Пример

Простой гармонический осциллятор без трения. Динамика такой структурно-неустойчивой системы описывается уравнениями

x'' + C₁ ⋅ x' + C₂ ⋅ x = 0
x(0) = a
x'(0) = 0

Нас будет интересовать влияние параметров C₁ и с C₂ на траекторию системы, причем из физических соображений ограничимся только случаями C₁ ≥ 0, C₂ > 0

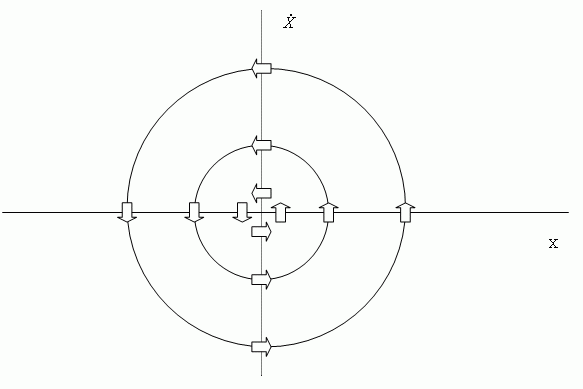
Рис.8.3 — Траектории осциллятора без трения

Рассматривая траекторию осциллятора на фазовой плоскости, легко видеть, что если C₁ = 0, то все траектории являются концентрическими окружностями с центром в начале координат. Если «ввести» в систему трение, то математически это означает, что C₁ > 0. Если C₁² > 4 ⋅ C₂, то точка равновесия х = 0 на плоскости есть узел, в противном случае это фокус.

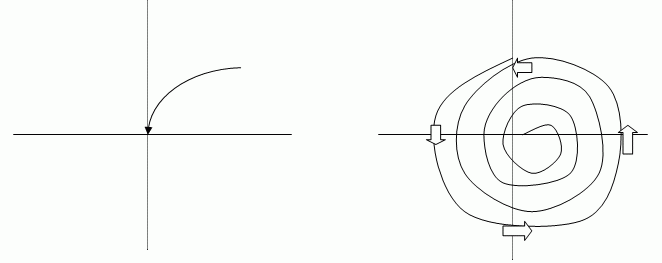
Рис.8.4 — Фазовый портрет траектории системы на плоскости

В обоих случаях начало координат является положением устойчивого равновесия по отношению к возмущениям в C₁ или C₂. Эта ситуация резко контрастирует со случаем системы без трения (C₁ = 0), когда начало координат есть центр и качественная картина поведения изменяется при сколь угодно малых изменениях C₁. Таким образом, при C₁ ≠ 0 система структурна устойчива в том смысле, что качественный характер положения равновесия (узел, фокус) сохраняется при малых изменениях структуры системы.

Поскольку идеи структурной устойчивости тесно связаны с поведением траекторий системы по мере приближения к ее состоянию равновесия, представляет интерес рассмотреть те области пространства состояний, которые соответствуют областям притяжения и отталкивания для данного состояния равновесия.

Иными словами, пусть задано равновесное состояние x*, для простоты считающееся фиксированным. Из каких начальных состояний система в конце концов придет в состояние x*? (Графически подобная ситуация изображена на рис.8.5)

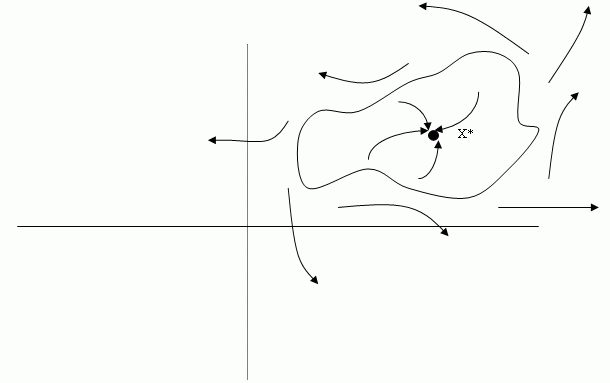
Рис.8.5 — Область притяжения фиксированной точки в R 2

Если допустить, что равновесные состояния могут быть предельными циклами или периодическими траекториями, то даже в двумерном случае картина может быть довольно сложной. В случае более высокой размерности картина еще более запутана. Тем не менее вопрос об описании областей устойчивости и родственные вопросы, связанные со структурной устойчивостью, изучены достаточно глубоко.

Пример более сложной структурно неустойчивой системы. Антисимметричная система хищник-жертва.

Предположим, что m видов взаимодействуют с популяцией i-го вида, численность которой N_i(t). Пусть a_i — коэффициент рождаемости i-го вида, а α_ij — коэффициент, характеризующий скорость уничтожения i-го вида j-м видом. Тогда динамика системы описывается уравнением Лотка-Вольтерра:

dN_i(t)/dt = N_i(t) ⋅ [a_i - ∑ α_ij ⋅ N_j(t)]

Нетривиальные равновесные популяции должны удовлетворять линейной системе алгебраических уравнений

∑α_ij ⋅ N_j* = a_i

При неочевидном предположении, что матрица является антисимметричной, можно показать, что при смещении системы из любого равновесного состояния, ее поведение будет чисто колебательным, поскольку собственные значения кососимметрической матрицы чисто мнимые. Следует отметить, что данное предположение означает, что коэффициент биохимического преобразования одного грамма жертвы j-го вида одинаков для всех хищников i-го вида, т.е. этот коэффициент не зависит от вида поедаемых особей. Можно показать, что величина

Q = ∑[N_i(t) - N_i* ⋅ log(N_i(t))]

постоянна вдоль любой траектории системы.

Этот закон сохранения есть следствие колебательного характера поведения системы и является аналогом закона сохранения механической энергии простого гармонического осциллятора, рассмотренного выше. Однако, как только кососимметричность матрицы А нарушается, состояния равновесия системы становятся узлами или фокусами (устойчивыми или неустойчивыми). В этом случае введение в систему сколь угодно малых изменений нарушает качественный характер траекторий, поэтому данная система структурно неустойчива. Более того, антисимметрические модели применимы только к системам с четным числом видов, поскольку из антисимметричности следует, что собственные значения матрицы А есть комплексно сопряженные числа. Если 3m 0 нечетно, то действительное собственное значение матрицы А должно быть равным нулю, что приводит к вырожденности матрицы взаимодействий. Таким образом, данная система является структурно неустойчивой и в смысле вариации ее размерности.

Катастрофы и адаптируемость

Положение равновесных состояний и соответствующих областей притяжения зависит от динамики изучаемой системы, поэтому важно знать, как они изменяются при небольшом изменении самой системы. Вопрос относительно того, приведет ли такое изменение к смещению данного состояния системы в другую область притяжения, представляет большой практический интерес, поскольку это привело бы к резким качественным изменениям в дальнейшем поведении системы. В качестве одного из инструментов исследования таких вопросов может быть использована теория катастроф.

Обычно в теории катастроф предполагается, что поведением изучаемого процесса управляет некоторая потенциальная функция, локальные минимумы которой соответствуют равновесным состояниям. Очень важно иметь в виду, что при таком подходе не обязательно точно знать, что это за функция — достаточно признать лишь сам факт ее существования. Предположим, далее, что можно измерять значения некоторых выходных переменных, генерируемых системой в ответ на входные воздействия. В «элементарной» теории катастроф предполагается, что все равновесные выходы фиксированы, т.е. фиксируют значения входных параметров и ждут пока не наступит равновесное состояние. Затем изменяют значения входных параметров и снова ждут и т.д. Поступая таким образом, получают поверхность равновесных состояний в пространстве выходов, которую можно изобразить как многозначную функцию входов. В первом приближении можно сказать, что «катастрофа» происходит тогда, когда возникает скачкообразное изменение выходных параметров при непрерывном изменении входов.

Для того чтобы связать эти рассуждения с нашими предыдущими замечаниями о важности анализа областей притяжения, заметим, что переход от одной области притяжения к области притяжения другого устойчивого состояния можно изобразить, как это показано на рис.8.6.

Точка x вначале принадлежит области притяжения состояния. Вследствие изменений динамики системы область притяжения Р сужается с I до II, а область притяжения Q расширяется с 1 до 2 . Теперь точка Х притягивается к Q, а не к P. Конечно, положения P и Q сами зависят от структуры системы, поэтому объекты, изображенные на этом рис. точками, по существу, являются областями, содержащими P и Q, но для нас важно лишь то, что область Р и Q отделены друг от друга. следовательно, возмущения в структуре системы, приводящие к изображенной выше ситуации порождают разрывы непрерывности в выходах, если наблюдаемые выходы оказываются равновесными состояниями.

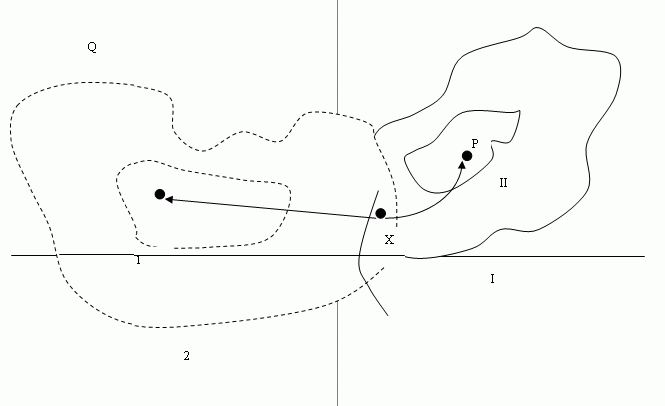
Рис.8.6 — Смещение областей притяжения

В заключение коснемся кратко понятия «адаптивности». Признано (в особенности экологами), что одним из наиболее желательных свойств системы является ее способность воспринимать внешние воздействия (ожидаемые или неожиданные) без необратимых фатальных изменений в ее поведении. Иными словами, адаптируемость в некотором смысле является мерой жизнеспособности или выживаемости системы. Естественно, для формулировки этого понятия в математических терминах необходимо точно определить, какие воздействия считаются «допустимыми» и что следует понимать под «выживаемостью». Тем не менее, даже такое интуитивное описание адаптируемости показывает, что это понятие тесно связано с понятием области притяжения и со смещением этих областей под действием естественных или искусственных возмущений. Если эти возмущения перемещают данное состояние системы в область притяжения «фатального состояния», то ясно, что система не обладает свойством адаптируемости по отношению к данному классу возмущений. В противном случае она в той или иной степени обладает этим свойством.

↑	Оглавление
←	Лекция 7, «Основные положения теории систем» (1 часть)	Лекция 9, «Сигналы в системах»	→