«Системный анализ и проектирование»

Е. Н. Живицкая

↑	Оглавление
←	Лекция 8, «Основные положения теории систем» (2 часть)	Лекция 10, «Энтропия и количество информации»	→

Лекция 9: Сигналы в системах

Современное понимание того, что такое информация и какую роль она играет в системном анализе, системах, сложилось не сразу. Оно представляет собой совокупность знаний, полученных разными науками: физикой, биологией, философией, теорией связи и т.д.

Известно, что физика старается изучать явления природы в максимально объективной форме, т.е. не связанной с человеком и его воздействием на окружающий мир. Однако ей (физике) не удается полностью исключить «человеческий фактор». Во-первых, при экспериментальном исследовании физических явлений невозможно обойтись без процедуры измерения ряда величин, параметров и процессов. Во-вторых, занимаясь изучением и разработкой технических (т.е. созданных человеком) устройств, физика не может обойтись без субъективного вмешательства человека. Впервые это произошло в термодинамике — науке, изучающей процессы в тепловых машинах. Оказалось, что без введения специального понятия энтропии невозможно дать исчерпывающего описания их действия. Скачок в понимании природы этой величины произошел, когда Л.Больцман дал ей статистическую интерпретацию (1877): энтропия характеризует недостающую информацию.

После построения К.Шэнноном теории информации (1948), обнаружилось, что формула Шэннона для информационной энтропии и формула Больцмана для термодинамической энтропии тождественны. Разгорелись споры о том, является ли это совпадение чисто формальным или оно выражает глубокую связь термодинамики и теории информации. Дискуссии привели к современному пониманию этой неразрывной связи.

Таким образом, ясно, что роль информации в самом существовании систем (искусственных и естественных) огромна. Для системного анализа понятие информации столь же фундаментально, как понятие энергии для физики. Более того, понятие информации, обладая всеобщностью, приобрело смысл философской категории. В настоящее время информация рассматривается как фундаментальное свойство материи.

Случайный процесс — математическая модель сигналов

Для того, чтобы два объекта содержали информацию друг о друге необходимо, чтобы между их состояниями существовало соответствие. Только при этом условии по состоянию одного объекта можно судить о состоянии другого. Такое соответствие может установиться только в результате физического взаимодействия между этими объектами. Соответствие между состоянием двух объектов может устанавливаться и с помощью взаимодействия с промежуточными объектами, например, сигналами. Сигнал есть материальный носитель информации, средство перенесения информации в пространстве и времени.

Сигналы играют в системах особую, очень важную роль. Если энергетические и вещественные потоки, образно говоря, питают систему, то потоки информации, переносимые сигналами, организуют все ее функционирование, управляют ею. Н.Винер, например, подчеркивал, что общество простирается до тех пределов, до каких распространяется информация. Пожалуй, это следует отнести к любой системе.

Первое и, быть может, главное отличие подхода к изучению объекта как системы и состоит в том, что мы не ограничиваемся только рассмотрением и описанием вещественной и энергетической его сторон, но и (прежде всего) проводим исследование его информационных аспектов: целей, сигналов, информационных потоков, управления, организации и т.д.

Казалось бы, после того, как мы установили, что сигналами служат состояния физических объектов, никаких проблем с их математическим описанием не должно быть. Например, можно зафиксировать звуковые колебания, соответствующие конкретному сигналу, в виде зависимости давления х от времени t и изобразить этот сигнал функцией x(t). Однако имеется существенное различие между просто состоянием x(t) объекта и сигналом x(t). Оно состоит в том, что единственная функция x(t) не исчерпывает всех важных свойств сигналов. Ведь понятие функции предполагает, что нам известно значение х (либо правило его получения) для каждого t. Если же это известно получателю сигнала, то отпадает необходимость в его передаче: функция x(t) может быть и без того воспроизведена на приемном конце.

Следовательно, единственная однозначная функция вещественного аргумента не может служить моделью сигнала. Такая функция приобретает сигнальные свойства только тогда, когда она является одной из возможных функций. Другими словами, моделью сигнала может быть набор (ансамбль) функций параметра t. Причем до передачи неизвестно, какая из них будет отправлена; это становится известным получателю только после передачи. Каждая такая конкретная функция называется реализацией. Если теперь еще ввести вероятностную меру на множество реализаций, то мы получим математическую модель, называемую случайным процессом.

Имеется несколько различных подходов к тому, как вводить вероятностную меру на множестве реализаций. Для большинства инженерных приложений оказывается удобным определение случайного процесса как такой функции времени x(t), значение которой в каждый момент времени является случайной величиной. Случайная величина полностью характеризуется распределением вероятностей, например, плотностью p₁(x₁,t₁). Однако, чтобы охарактеризовать случайный процесс, нужно знать, как связаны значения реализации, разделенные некоторыми интервалами времени. Для этих целей вводят распределения второго, третьего, ..., n-го порядков p_n(x₁,t₁,...,x_n,t_n).

Для рассмотрения конкретных свойств систем бывает необходимо учесть особенности сигналов, циркулирующих по каналам связи этих систем. Такие особенности можно описать по-разному: просто перечислить возможные реализации (если число их конечно), либо задать в той или иной форме общие свойства реализаций, входящих в ансамбль. Рассмотрим в качестве примеров некоторые модели реализаций непрерывных сигналов.

Моделирование конкретных реализаций

Гармонические сигналы

Обозначим через A_c множество всех синусоидальных сигналов:

Ac = {x(t) = Ac ⋅ cos(w⋅t + y)}

{9.1}

здесь R — множество всех положительных действительных чисел; А — амплитуда, w — круговая частота, y — фаза гармонического колебания.

Модулированные сигналы

В технических системах полезная информация может переноситься каким-нибудь одним параметром «гармонического» колебания. Конечно, при изменении этого параметра во времени колебание перестает быть гармоническим. Процесс изменения параметра колебания называется модуляцией, а выделение этого изменения в «чистом виде» — демодуляцией. Само колебание называется несущим. Различают амплитудную, частотную и фазовую модуляции в зависимости от того, на какой из параметров несущего колебания «накладывают» полезную информацию:

Aам = {x(t) = A(t) ⋅ cos[w0⋅t + y0]} Aчм = {x(t) = A0 ⋅ cos[w(t)⋅t+ y0]} Aфм = {x(t) = A0 ⋅ cos[w0⋅t + y(t)]}

{9.2}

Необходимо отметить, что физический смысл модуляции сохраняется лишь в том случае, когда модулирующий сигнал является «медленно меняющимся» по сравнению с несущим колебанием. Только при этом условии можно говорить о гармоническом сигнале с переменной амплитудой, частотой либо фазой.

Сигналы с ограниченной энергией

О сигналах из множества A_э = {x: ∫x(t)dt ≤ K < ∞} говорят, что их энергия ограничена величиной К. Происхождение этого названия связано с тем, что если x(t) есть напряжение, то интеграл представляет собой энергию, выделяемую сигналом x(t) на единичном сопротивлении.

Сигналы с ограниченной полосой частот

Фурье-преобразование X(f) сигнала x(t) называют его спектром:

X(f) = ∫x(t)⋅exp[j2πft]dt.

Физический смысл спектра состоит в том, что колебание x(t) представляется в виде суммы (в общем случае в виде интеграла) составляющих его гармонических колебаний с определенными амплитудами |X(f)| , частотами и соответствующими фазами. Между x(t) и X(f) имеется взаимно однозначное соответствие, так как

x(t) = ∫X(f)⋅exp[-j2πft]df.

Условием существования и обратимости Фурье-преобразования является ограниченность энергии сигнала (интегрируемость в квадрате функций x(t) и X(f)).

Если функция X(f) на оси f имеет ограниченный носитель F, то говорят, что сигнал x(t) имеет ограниченную полосу частот шириной F:

A_F = {X(f) = ∫x(t)⋅exp[j2πft]dt = 0 для всех f ≥ |F|}

Частотно-временное представление сигналов

Мы излагаем только элементы теории сигналов, преследуя при этом ознакомительные цели. В то же время представляется интересным рассмотреть два основных ее аспекта, относящихся к свойствам непрерывных сигналов. Первый — это частотно-временная неопределенность сигналов.

Как мы уже отметили, сигнал x(t) и его спектр X(f) однозначно выражаются друг через друга. Следовательно, сигнал можно рассматривать в любом из этих эквивалентных представлений — временном или частотном. При этом масштабные параметры этих представлений связаны обратно пропорциональной зависимостью. Допустим, что изменили масштаб по оси времени в k раз (например, воспроизведем запись x(t) с другой скоростью) и найдем спектр функции x(k⋅t):

X_k(f) = ∫x(k⋅t)⋅exp[j2πft]dt = (1/k)⋅X(F/k)

Как видим, масштаб по частотной оси изменился в 1/k раз. Более того, из свойств преобразования Фурье следует, что сигналы с ограниченной длительностью имеют спектры неограниченной ширины, а сигналы с ограниченной полосой частот длятся бесконечно долго. Этот математический результат находится в противоречии с практикой: в реальности все сигналы конечны по длительности и ограничены по спектру. Тот факт, что аналитическая функция времени не может быть одновременно ограниченной и по длительности и по ширине спектра является, как видим, не свойством реальных сигналов, а свойством данной модели сигналов.

Говорить об одновременной ограниченности сигналов по времени и по спектру оказывается возможным при использовании энергетического критерия точности: сигнал считается имеющим конечную длительность Т, если в этом интервале времени сосредоточена основная часть всей энергии функции x(t). В то же время и ширина спектра F сигнала определяется как область частот, содержащая эту же часть всей энергии спектра X(f):

∫x²(t)dt = ∫|X(f)|df = μ∫x²(t)dt = μ∫|X(f)|df

Здесь величина M меньше единицы, хотя достаточно близка к ней, а величина 1-M характеризует косвенным образом точность, о которой шла речь.

Теперь можно говорить о том, какую «площадь» на плоскости «частота-время» занимает тот или иной сигнал. Если строго следовать теории Фурье-преобразований, то получим, что эта площадь для всех сигналов бесконечна. Но для большинства из них энергетический критерий позволит ограничить ее естественным образом.

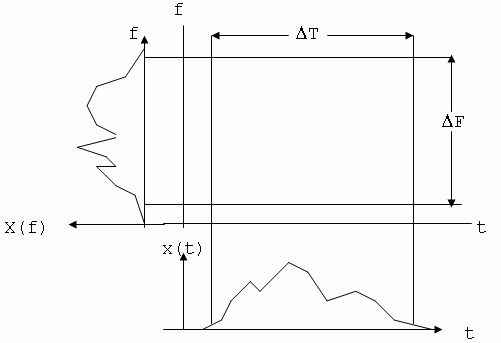
Рис.9.1 — Иллюстрация частотно-временной неопределенности сигнала

Меняя форму сигнала, можно изменить и площадь на плоскости «время-частота», которую он занимает. Оказывается, что уменьшать эту площадь можно лишь до некоторого предела. Этот предел достигается на кривой, являющейся гармоническим колебанием, которое модулировано по амплитуде гауссовым импульсом. Существование предела, ниже которого нельзя сжать площадь сигнала, занимаемую им на плоскости «частота-время», и называется (по аналогии с принципом неопределенности в квантовой механике) принципом частотно-временной неопределенности сигналов:

ΔF ⋅ ΔT = const ≥ 0

Дискретное представление сигналов

Вторым важным аспектом теории сигналов является проблема дискретного представления непрерывных сигналов. Вопрос формулируется так: существуют ли условия (и если да, то каковы они), при которых любой непрерывной функции x(t) можно поставить во взаимно однозначное соответствие дискретное множество чисел {C_k(x)}, k =...-2,-1,0,1,2,...

Положительный ответ на этот вопрос имел бы как теоретическое, так и практическое значение. Во-первых, рассмотрение случайных величин вместо реализаций непрерывных случайных процессов существенно упрощает решение многих задач, теория становится проще и может быть продвинута дальше.

Во-вторых, соответствие значения x(t) значению {C_k(x)}можно использовать в технических устройствах, работающих с непрерывными сигналами.

Ограничимся более конкретной формулировкой поставленной задачи и рассмотрим условия выполнения равенства

x(t) = ∑_kC_k(x)⋅φ_k(t).

Функции φ_k(t) называются координатными функциями, они не должны зависеть от x(t), более того, они заранее известны. Ряд в правой части равенства называется разложение x(t) по координатным функциям. Числовые коэффициенты {C_k(x)} содержат всю информацию об x(t), необходимую для восстановления этой функции по формуле (5.7), следовательно, {C_k(x)} являются функционалами от функции x(t) (функционалом называется отображение множества функций в множество чисел).

Наиболее известны разложения по системе ортогональных и нормированных функций. Это означает, что функции φ_k(t) удовлетворяют условиям

∫φ_i(t)⋅φ_kdt = 1 при i = k
∫φ_i(t)⋅φ_kdt = 0 при i ≠ k

Умножим обе части равенства (5.7) на i(t) и проинтегрируем

∫φ_i(t)⋅x(t)dt = ∑_kC_k(x)⋅∫φ_i(t)⋅φ_k(t)dt

Такое представление называют рядом Фурье, а {C_k(x)} — коэффициентами Фурье. Условия сходимости ряда Фурье к функции x(t) подробно исследованы и, кратко говоря, сводятся к тому, чтобы были оправданы все необходимые математические операции, а коэффициенты Фурье убывали достаточно быстро.

Значительный интерес привлекли разложения реализаций случайного процесса с ограниченной полосой частот. Для таких сигналов Котельников доказал (1946г.) следующую теорему (теорему отсчетов): любая функция со спектром, находящимся в интервале [0,F], полностью определяется последовательностью ее значений в точках, отстоящих друг от друга на 1/(2⋅F) единиц времени.

x(t) = ∑x(k/2⋅F)⋅{[sin(2⋅π⋅F⋅t - k⋅π)]/(2⋅π⋅F - k⋅π)}

Т.е. мы имеем разложение реализации координатными функциями вида [sinu] /u, сдвинутые относительно друг друга на интервалы времени 1/(2⋅F), с коэффициентами, равными отсчетам самой реализации, взятые в моменты t = k/(2⋅F).

Подведем итог

Из многочисленных результатов теории сигналов мы выделяем два, как существенно проясняющих природу непрерывных сигналов.

Первый состоит в том, что сигналы обнаруживают своеобразную «упругость» занимаемой ими площади на плоскости «время-частота». Это явление называется частотно-временной неопределенностью сигналов.

Второй результат заключается в том, что определенный класс непрерывных сигналов допускает взаимно однозначное соответствие между любой реализацией из этого класса и дискретным набором отсчетов данной реализации.

↑	Оглавление
←	Лекция 8, «Основные положения теории систем» (2 часть)	Лекция 10, «Энтропия и количество информации»	→