«Системный анализ и проектирование»

Е. Н. Живицкая

↑	Оглавление
←	Лекция 18, «Методология решения слабо структуризованных проблем»	Лекция 20, «Принятие решений в процессе системного проектирования»	→

Лекция 19: Основы принятия решений при многих критериях

Постановка задачи векторной оптимизации и классификация многокритериальных методов

В упрощенном виде задача векторной оптимизации формируется следующим образом:

Имеется n конкурирующих решений:

{S_i} = {S₁, S₂, ..., S_n}, т.е. стратегий, структур, проектов, плакатов и т.д. и m частных критериев

{K_j} = {K₁, K₂, ..., K_m}, не всегда согласованных между собой и противоречивых.

Для оценки конкурирующих решений по частным критериям используются различные средства: экспертные процедуры, мат. моделирование, натуральные эксперименты. При этом множество конкурирующих решений отображается в матрицу векторных оценок:

	S1	S2	...	Sn
[kji] =	k11	k12	...	k1n
	k21	k22	...	k1n
	...	...	...	...
	km1	km2	...	kmn

Исходя из матрицы векторных оценок и системы предпочтений ЛПР выбирается рациональное решение.

E = opt_Sj {[k_ji], система предпочтений ЛПР} следовательно S_rat

opt — некоторый оператор векторной оптимизации.

Выбор рационального решения связан с преодолением неопределенностей, которые имеются в связи с наличием многих критериев. Эта неопределенность является принципиальной. Для ее компенсации есть лишь одна единственная возможность: использование системы предпочтений ЛПР (т.е. дополнительной, субъективной информации).

Использование субъективной информации ЛПР позволяет преодолеть принципиальные трудности и выбрать рациональный критерий.

Все множество методов векторной оптимизации можно разбить на 5 классов.

1. Методы, основанные на формализации, в виде задач математического программирования.
2. Методы, основанные на реинжинировании критериев и их последовательном применении.
3. Методы, использующие обобщенный критерий для сравнительной оценки альтернатив.
4. Методы, не использующие обобщенный критерий для сравнительной оценки альтернатив.
5. Методы, реализующие процессы структуризации и адаптации при выборе рациональных решений.

Методы расположены в порядке возрастания их потенциальной характеристики (классификационный признак — полнота реализации принципа системности). Методы 1-го и 2-го класса не реализуют в полной мере принцип системности. Методы 3-го класса достаточно конструктивны (их легко использовать), однако не всегда удается обосновать и построить обобщенный критерий. Методы 4-го класса более прогрессивны, т.к. они предусматривают активное использование ЛПР в процессе анализа альтернатив. Методы 5-го класса отражают современные тенденции в области векторной оптимизации и находят применение в современных перспективных интерактивных автоматизированных системах.

АСНИ, САПР, АСЛПР, ... поддержки принятия решений.

1-3 — используют;

4-5 — разрабатывают (в том числе и на нашей кафедре).

Принцип согласованного оптимума В.Парето

В.Парето обосновал принцип согласованного оптимума, ориентируясь на конфликтную ситуацию между несколькими субъектами с пересекающимися интересами (1870 г). Согласованный оптимум означает преобразование конфликтной ситуации в такую ситуацию, в которой ни один из участников конфликта не может улучшить свое состояние, не причинив своими действиями вреда партнерам. Состояние согласованного оптимума является наилучшим для всех взаимодействующих субъектов. Леонард Заде распространил принцип согласованного оптимума на технические системы (1963 г).

В процессе их проектирования стремятся оптимизировать систему по многим, часто противоречивым критериям. Однако оптимизация системы по одному из критериев практически исключает возможность оптимизации по другим критериям. Поэтому важно найти согласованный оптимум для всех используемых критериев.

Если векторная оптимизация осуществляется с использованием обобщенного критерия, то реализуются обычно следующие процедуры:

1. Выполняется обоснование способа свертки частных критериев в обобщенный критерий.
2. Учитывается важность частных критериев.
3. Векторные оценки приводятся к безразмерному виду.
4. Для всех конкурирующих решений вычисляются обобщенные скалярные оценки.
5. Определяется область компромисса, содержащая парето-оптимальные решения (т.е. такие решения, когда улучшения состояния по каждым из критериев ухудшает состояние по другим критериям).
6. Выбирается рациональное решение в области компромиссов с учетом системы предпочтений ЛПР.

Приемы поиска Парето-оптимальных решений

Пример 1: определить Парето-оптимальные варианты системы

{Kj}	Единица измерения	Направление экстремума	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10
K1 — масса	K2	min	13	5	11	2	10	16	12	15	9	5
K2 — стоимость	рубли	min	200	900	400	800	700	200	500	500	1100	1100

Явно видно, что вариант S₁₀ можно выбросить, т.к. S₂ — дешевле. S₆ — можно забраковать и оставить первый вариант, а остальные сравниваем с оптимальными (т.е. 3, 4 и т.д. с 1 и 2). Найдем граничные варианты в области компромисса: S₁ и S₂, причем варианты S₆ и S₁₀ необходимо отбраковать как худшие.

Определим Парето-оптимальные варианты системы.

S₁, S₂, S₃, S₄, S₅, S₇

S₈, S₀ выбросим

Произвести дальнейший отбор.

Пример 2: Определить парето-оптимальные варианты системы, которая состоит из блоков А и В

{Kj}	Единица измерения	Направление экстремума	Блок A						Блок B
			A1	A2	A3	A4	A5	A6	B1	B2	B3	B4	B5
K1 — масса	K2	min	6	7	5	17	14	15	10	6	6	15	17
K2 — стоимость	рубли	min	800	600	500	300	200	250	500	400	300	200	300

Определим Порето-оптимальные варианты системы S₁, S₃, S₄

Пример 3: выбрать рациональный вариант системы в условиях, когда ЛПР применяет минимальный критерий

{Kj}	Единица измерения	Направление экстремума	{Si}
			S1	S2	S3	S4	S5	S6
K1 — вероятность отказа	—	min	1,2⋅10-2	0,5⋅10-2	0,3⋅10-2	0,1⋅10-2	0,08⋅10-2	0,05⋅10-2
K2 — затраты ресурсов	тысячи рублей	min	200	400	600	900	1200	1500
Ограничения для системы K1 ≤ 1⋅10-2, K2 < 1 млн. руб.

Определим Парето-оптимальные варианты системы и матрицу потерь

Zji	S2	S3	S4
K1	0,5	0,3	0,1
K2	0,4	0,6	0,9

min_Si(max_Kj(Z_ji)) = min{0,5; 0,6; 0,9} = 0,5

Т.е. рациональным является вариант системы S₂.

Общая технологическая схема принятия решений при многих критериях

Принятие решений является наиболее массовой операцией в процессе создания некоторой АСУ практически на всех ее этапах.

1. Оценка целесообразности разработки и предварительный выбор структуры АСУ.
2. Предварительный выбор технических решений.
3. Окончательный выбор структуры АСУ.
4. Окончательный выбор технических решений по построению п/с и АСУ в целом.
5. Окончательный выбор технических решений по созданию аппаратуры.
6. Окончательный выбор технических решений по разработке математического обеспечения.
7. Организация АСУ на базе выбранных технических решений.
8. Отладка, испытание и внедрение АСУ.

См. общее системное проектирование АСУ реального времени. Под редакцией В. А. Шабалина, М., радио и связь, 1984 г, стр.34-44.

Принятие решений при многих критериях базируются на принципе согласованного оптимизма В.Парето и представляет собой многошаговый интеративный процесс, который начинается с появлением проблемы и заключается реализацией решений.

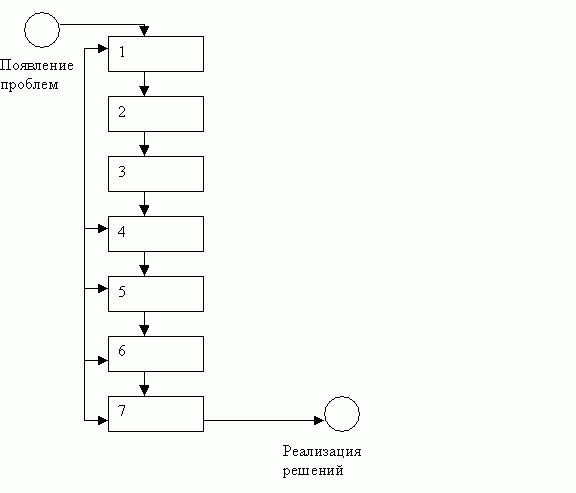
Рис. 19.1  —  Принятие решения

1. Сбор исходных данных и структуризация проблемы:

   а) ограничение сложности

   б) отображение ситуации

   г) оценка ресурса

   д) выявление взаимосвязей

2. Выявление и систематизация потенциальных возможных решений
3. » Просеивание» решений, выделение множества конкурирующих решений
4. Обоснование частных критериев для оценки конкурирующих решений
5. Построение логико-математической системной модели и ее верификации

6. Выбор рационального решения, которые должны быть:

   а) единственным

   б) своевременным

   в) реализуемым

   г) устойчивым

   д) перспективным

Циклы проектирования и уровни оптимизации сложных технических систем

В настоящее время в стадии становления находится новое научное направление, а именно т-я качества сложных систем, в частности АСУ различных уровней и назначения. В проблематику данного направления входят вопросы обеспечения качества систем на всех этапах их создания и развития. Современное представление о процессе проектирования сложных технических систем включает 3 характерных цикла:

1. внешнее проектирование
2. формирование облика системы
3. внутреннее проектирование

Первый цикл представляет конкретизацию целей и функций системы, а также представление требований к ее характерам качества.

Второй цикл служит для корректной увязки требований внешнего проектирования с конструкторскими и технологическими возможностями внутреннего проектирования и состоит в выборе рациональной структуры из некоторого множества конкурирующих структур.

Третий цикл предполагает разработку выбранной структуры и ее реализацию в виде комплекса технических ф-в, принадлежащих системе требуемое качество.

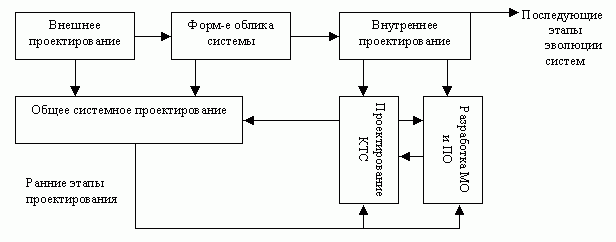
Рис.19.2  —  Циклы проектирования технических систем

Циклам проектирования соответствуют следующие уровни оптимизации систем:

1. Глобальная оптимизация, т.е. поиск прогрессивной технической идеи для создаваемой системы.
2. Структурная оптимизация, т.е. выбор рациональной структуры системы в рамках используемой технической идеи.
3. Параметрическая оптимизация, т.е. подбор наилучшей совместимости параметров для выбранной структуры систем.

Оптимизация системы последовательно на всех 3-х уровнях приводит к синтезу структуры, удовлетворяющей заданным требованиям по качеству.

Наибольший эффект в обеспечении качества системы дает глобальная оптимизация (Глушков, Мясников, Половинкин) 30-50%, наименьший эффект — параметрическая оптимизация 10-15%, структурная оптимизация занимает промежуточное положение 20-30%. Причем, степень оптимизации зависит весьма существенно от множества конкурирующих структур и их проработки по векторному критерию качества.

Структурная оптимизация систем, как процесс принятия решений

Необходимость структурной оптимизации обусловлена наличием сравнительно большой номенклатуры технических средств и способов, объединяя их в различные структуры, которые отличаются друг от друга рядом признаков, а именно, составом структурных элементов, технологией переработки информации, пространственным распространением элементов и др.

Анализ конкурирующих структур неизбежно связан с использованием многих критериев и выполняется в условиях неопределенности, т.е. в условиях неполноты информации в отношении создаваемой системы и внешней среды, взаимодействующей с ней. По этой причине проблема структурной оптимизации формируется как проблема многокритериального выбора рациональной структуры из некоторого множества конкурирующих структур в условиях неопределенности. Проблема структур оптимизации в такой постановке решается на основе методологии системного анализа.

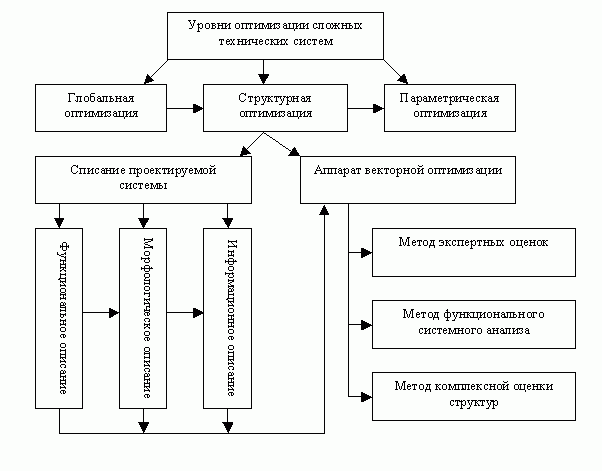
Рис.19.3  —  Уровни оптимизации систем

В процессе структурной оптимизации необходимо осуществлять целенаправленный поиск альтернативных структур, т.к. их случайный перебор обычно не приводит к успеху. При этом, чем больше альтернативных структур, тем с большей вероятностью можно гарантировать конечный результат, т.е. выбор наиболее рациональной структуры. Вместе с тем, большой объем альтернативных структур порождает проблему отсева (отбраковки) неперспективных структур, исходя из тех или иных ограничений и требований к системе.

Таким образом процесс структурной оптимизации — это процесс систематизации альтернативных структур с отсевом неперспективных структур и определение множества конкурирующих структур, из числа которых выбирается рациональная структура.

Метод ФСА (функционально-стоимостного анализа)

Метод предусматривает 2-хкритериальную оценку вариантов системы и включает в себя 5 основных операций:

1. построение модели эффективности
2. построение модели стоимости
3. вычисление обобщенного критерия
4. выбор рационального варианта

Поясним сущность метода на примере ВЦ с распределенной сетью терминалов. В этом случае возможно построить следующие модели:

1. Э = f(n)-коэффициент загрузки ‚– в зависимости от числа используемых терминалов.
2. Стоимость функции от n: С = f(n) — затраты на создание ВЦ в зависимости от числа используемых терминалов.

При построении моделей используется вся доступная объективная и субъективная информация. Выходные данные модели в соответствии с методом синтезируются в обобщенный критерий, позволяющий анализировать варианты системы. Базируясь на обобщенных оценках, ЛПР выбирает рациональный вариант системы.

Сложно в ФСА построить модель эффективности. В качестве обобщенного критерия Е можно использовать:

1. E = max Э при С = const — максимум эффективности при фиксированной стоимости.
2. E = min C при Э = const — минимум стоимости при фиксированной эффективности.
3. E = max Э/С — минимум удельной эффективности.
4. E = min C/Э — минимум удельной стоимости
5. E = max (w1Э + w2С) — максимум взвешенной суммы эффективности и стоимости.

Выбор обобщенного критерия Е осуществляется, как правило, на основе субъективных суждений ЛПР. 3 — применяется на практике наиболее часто (т.к. наиболее понятно; получаем число, которое никакого смысла не имеет; выбираем число с максимальным значением).

Метод комплексной оценки структур

Метод служит для решения задач структурной многокритериальной оптимизации систем в процессе их проектирования или модернизации. Базируется на методологии системного анализа и представляет собой многошаговый итерактивный процесс, который начинается с формулировки целевого назначения системы и заканчивается выбором рациональной структуры. Этот процесс не поддается полной математической формализации и поэтому представляет собой сложную цель эвристических и формальных процедур. Сочетание эвристики и формализма образует системный метод, дисциплинирующий решение проектировщика и позволяющий решать широкий класс задач многокритериального выбора рациональной структуры.

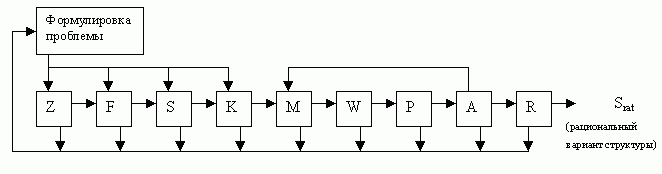
Рис.19.4  —  Комплексная оценка структур

Концептуальная схема метода включает следующие операторы:

Z — цель системы достигается в процессе функционирования при взаимодействии с внешней средой;

S — конкурирующие структуры, выявляемые в результате морфологического анализа;

K — частные критерии, характеризующие качество конкурирующих структур;

М — совокупность моделей, позволяющих оценить отдельные свойства конкурирующих структур;

W — векторные оценки, получаемые для конкурирующих структур по частным критериям;

Р — процедуры скаляризации, направленные на свертку векторных оценок по каждой из структур;

А — анализ структур, осуществляемый на основе обобщенных скалярных оценок в диапазоне условий;

R — решающее правило, определяющее выбор рациональной структуры в заданном классе условий.

Практическое применение метода требует расшифровки операторов с учетом особенностей конкретной системы. При этом выполняется 6 основных операций:

1. Определение множества конкурирующих структур исходя из целей и функций системы. Эта задача накрывает эти операторы (Z, F, S).
2. Отбор совокупности частных критериев, характеризующих качество конкурирующих структур (К).
3. Построение модели и отображение конкурирующих структур в матрицу векторных оценок (М, W).
4. Обоснование принципа оптимальности и свертка векторных оценок в обобщенные скалярные оценки (Р).
5. Анализ конкурирующих структур в диапазоне условий, в частности при различных воздействиях внешней среды (А).
6. Разработка решающего правила и выбор на его основе рациональной структурной системы (R).

Методика многокритериального выбора рациональных структур

Рассмотрим методику, которая реализует все операторы метода комплексной оценки структур (т.е. более подробно, чем сам метод).

Операторы метода	Z, F, S	K	M, W	P	A	R
Этапы методики	1	2	3	4-10	11	12

Этап 1:

Определяется множество конкурирующих структур {S_i} = {S₁, S₂, ..., S_n}, из числа которых выбирается в дальнейшем рациональная структура. Для поиска структур могут быть использованы различные методы: мозговой атаки; дерево целей; морфологического ящика и др. На практике закрепился метод морфологического ящика (анализа). Морфологический анализ создаваемой системы позволяет систематизировать потенциально возможные структуры и определить множество конкурирующих структур.

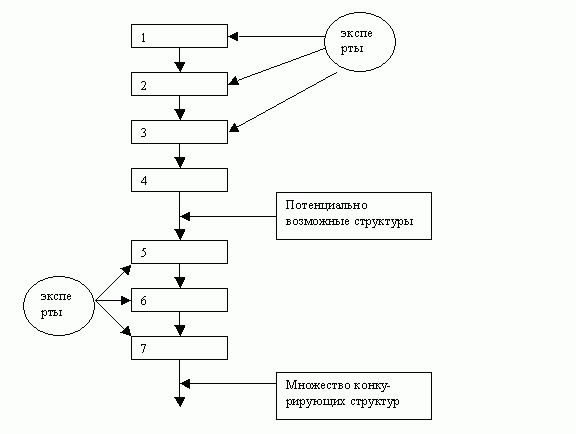
Рис.19.5 — Множество конкурирующих структур

Этап 1

1. Формируется целевое назначение системы
2. Выявляются ее основные функции
3. Составляется морфологическая матрица

4. Вводятся ограничения

   а) экономические

   б) технические

   в) эксплуатационные

5. Выполняется проверка структур на допустимость

Этап 2:

Отбирается совокупность частных критериев {K_i} = {K₁, K₂, ..., K_m}, которые служат для оценки качества конкурирующих структур.

Набору критериев предъявляется ряд требований:

1. полнота, т.е. набор критериев должен охватывать все ватные аспекты решаемой задачи;
2. операционность, т.е. каждый критерий должен характеризовать вполне определенное свойство системы;
3. измеримость, т.е. каждый критерий должен допускать оценку интенсивности характеризуемого им свойства;
4. декомпозируемость, т.е. критерий набора должен обеспечивать возможность разложения задачи на части с меньшей размерностью;
5. неизбыточность, т.е. критерии набора не должны учитывать один и тот же аспект последствий;
6. минимальность, т.е. набор критериев должен содержать как можно меньшее число критериев.

Противоречивость требований заставляет искать компромисс при построении набора критериев.

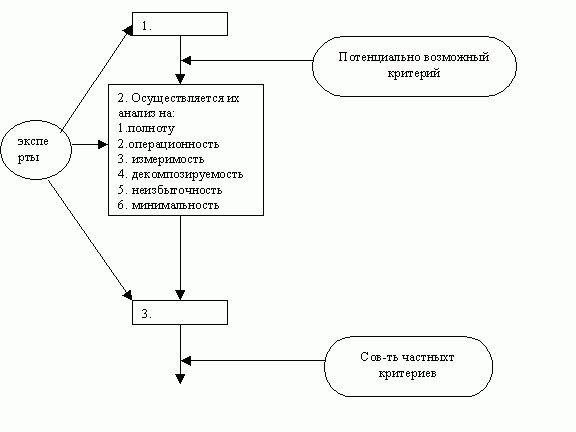
Рис.19.6 — Набор критериев

Этап2

1 — формируется полный перечень частных критериев;

3 — выполняется отбор критериев и их обоснование.

Этап 3:

Выполняется оценка конкурирующих структур по частным критериям для М-ого варианта условий

Для оценки структур используются все возможные средства, которые имеются в наличии на данный момент эволюции систем: аналитические, имитационные, полунатурные модели, полунатурные испытания, проведение экспертиз.

Получаемые оценки K_ji^(M) образует матрицу критерии структуры

{Kj}	Единицы измерения	Направление экстремума	{Si}
			S1	S2	...	Sn
K1	...	...	K11(M)	K12(M)	...	K1n(M)
K2	...	...	K21(M)	K22(M)	...	K2n(M)
...	...	...	...	...	...	...
Km	...	...	Km1(M)	Km2(M)	...	Kmn(M)

Этап 4:

Составляется матрица бинарных предпочтений ЛПР, которое содержит результаты попарных сравнений критериев по важности. 1 — если критерий строки считается более важным, чем критерий столбца. 0 — в противном случае. 0,5 — если критерии не сравнимы по важности.

Суммирование оценок по строке определяет цену критерия.

{Ki}	K1	K2	...	Km	Cj(M)
K1	...	...	...	...	...
K2	...	...	...	...	...
...	...	...	...	...	...
Km	...	...	...	...	...

Вылавливаем, что у ЛПР «в голове»

Этап 5:

Находятся веса частных критериев, отражающие неформальное отношение ЛПР

ϑ_1j = C_j^(M)/∑r_j^(M), j = 1,m

Этап 6:

Находятся веса частных критериев, исходя из разброса векторных оценок

ϑ_2j = Z_j^(M)/∑r_j^(M), j = 1,m

r_j^(M) = 1/n⋅(∑(-[k_ji^(M) - k_ji^(M)^]/k_ji^(M)^))

k_ji^(M) = ∑k_ji^(M)/n

Этап 7:

Находятся обобщенные веса частных критериев в классе линейных функций

ω_j^(M) = a⋅ϑ_1j^(M) + b⋅ϑ_2j^(M), j = 1,m

где а и b — это коэффициенты, характеризующие степень доверия к соответствующим весам.

a + b = 1

В частном случае, когда a = b = 0,5

ω_j^(M) = 0,5⋅(ϑ_1j^(M) + ϑ_2j^(M)), j = 1,m, ∑ω_j^(M) = 1

Этап 8:

Оценки матрицы критериев структуры приводятся к безразмерному виду.

ρ_ji^(M) = k_ji^(M)/Δk_j

Δk_j значение-кванты по частному критерию K_j, причем под квантой понимается мера разумной точности измерения соответствующей характеристики.

Этап 9:

Формируется матрица взвешенных оценок

E_ji^(M) = ω_j^(M)⋅ρ_ji^(M) (j = 1,m, i = 1,n)

Этап 10:

Вычисляются обобщенные скалярные оценки

q_i^(M) = ∑l_ji(max) - ∑l_ji(min) (i = 1,n)

т.е. находится разность суммарных взвешенных оценок по критериям, подлежащим соответственно, минимизации и максимизации.

Этап 11:

при оценке структур в диапазоне условий осуществляется η-кратное повторение этапов 3-10. В результате получаем матрицу структуры условий.

{Si}	{M}
	1	2	...	η
S1	q1(1)	q2(1)	...	q1(2)
S2	q2(1)	q2(2)	...	q2(2)
...	...	...	...	...
Sn	qn(1)	qn(2)	...	qn(2)

Для первого варианта воздействия

Этап 12

На основе матрицы структуры условия выбирается рациональная структура системы. Эта структура должна обладать приемлемой эффективностью для всех вариантов условий, возникающих с вероятностями p_M. Для известных вероятностей p_M, имеющих частотную или субъективную трактовку, целесообразно использовать критерий максимума средней эффективности в диапазоне условий.

E = max_Si(∑q_i^(M)⋅p_M) ⇒ S_rat

На практике типичной является ситуация, когда вероятности p_M не известны. В данном случае используются критерии для выбора решений в условиях неопределенности.

Структурная оптимизация локальной информационно-вычислительной сети

Применим методику многокритериального выбора рациональных структур, для структурной оптимизации локальной информационно-вычислительной сети (ИВС). Локальная ИВС содержит вычислительную систему, которая может включать несколько однотипных процессоров (на сколько процессоров?) и N распределенных по региону терминалов пользователей, имеющих теледоступ к ИВ ресурсам этой системы.

Необходимо на реальных данных определить число процессоров.

Этап 1: Множество конкурирующих структур

{S_i} = {S₁, S₂, S₃}, где S₁, S₂, S₃ имеют следующий смысл:

S₁ — структура с одним процессором;

S₂ — структура с двумя процессорами;

S₃ — структура с тремя процессорами.

Этап 2: Совокупность частных критериев

{K_j} = {K₁, K₂, K₃, K₄, K₅}, где

K₁ — время реакции системы;

K₂ — коэффициент загрузки процессора;

K₃ — пропускная способность системы;

K₄ — вероятность правильного ответа;

K₅ — стоимость процессорных устройств.

Этап 3: Матрица критерии структуры:

{Kj}	Единицы измерения	Направление экстремума	N = 10			N = 20			N = 30			N = 50
			S1	S2	S3	S1	S2	S3	S1	S2	S3	S1	S2	S3
K1	Сек	min	2,89	2,08	2,05	5,7	2,89	2,71	11,5	4,38	3,38	25,8	9,64	0,99
K2	%	max	55	30	20	91	55	37	99,8	75	51	100	91	63
K3	Задач/сек	max	0,78	0,83	0,83	1,27	1,55	1,57	1,4	2,09	2,15	1,4	2,55	2,69
K4	—	max	0,85	0,95	0,99	0,85	0,95	0,99	0,85	0,95	0,99	0,85	0,95	0,99
K5	Тыс. руб.	min	340	490	640	340	490	640	340	490	640	340	490	640

Чтобы получить количественные средства, нужно использовать все возможные средства (например, аналитические вычисления).

Покажем расчеты для N = 20

{Ki}	K1	K2	K3	K4	K5	Cj
K1		1	0,5	0	0,5	2
K2	0		0,5	0	0	0,5
K3	0,5	0,5		0	0	1
K4	1	1	1		0,5	3,5
K5	0,5	1	1	0,5		3

∑C_j = 10

Этап 6: Веса частных критериев исходя из разброса векторных оценок для N = 20

суммируем по строке 3

{Ki}	Kji^	rj	ϑ2j
K1	3,77	0,34	0,33
K2	61	0,33	0,32
K3	1,46	0,09	0,09
K4	0,93	0,06	0,06
K5	490	0,2	0,2

0,34 = (/5,7 - 3,77/ + /2,89 - 3,77/ + /2,71 - 3,77/3,77)/3

Наибольший вес в формальном способе расчета имеет время реакции системы. Далее — все наоборот (не так, как дал человек).

Этап 7: Усредненные веса частных критериев для N = 20

ω₁ = 0,27( = 0,265) а = b = 0,5

ω₂ = 0,18 Наиболее важным получился критерий K₁

ω₃ = 0,09

ω₄ = 0,21

ω₅ = 0,25

Этап 8: Матрица безразмерных векторных оценок для N = 20

{Kj}	ΔKj	Единица измерения	{Si}
			S1	S2	S3
K1	0,5	Сек	11,4	5,78	5,42
K2	5	%	18,2	11	7,4
K3	0,25	Задач/сек	5,08	6,2	6,28
K4	0,1	—	8,5	9,5	9,9
K5	100	Тыс. руб.	3,4	4,9	6,4

т.е. делим на кванту то число, которое стоит в таблице матрицы критериев структуры

Кванта — это тот «кирпичик», через который человек чувствует этот критерий 0,5 — т.е. через 0,5 сек человек начинает чувствовать эту характеристику.

Этап 9: Матрица взвешенных векторных оценок для N = 20

{Kj}	ωj	Направление экстремума	{Si}
			S1	S2	S3
K1	0,27	min	3,08	1,57	1,46
K2	0,18	max	3,28	1,98	1,33
K3	0,09	max	0,46	0,51	0,57
K4	0,21	max	1,78	1,99	2,03
K5	0,25	min	0,85	1,22	1,6

Эти веса умножаем на столбик прошлой матрицы

 = 0,27⋅11,4

Этап 10: обобщенные скалярные оценки для N = 20

q₁ = 1,59; q₂ = 1,74; q₃ = 0,92.

Этап 11: матрица структуры условия:

{Si}	{M}
	N = 10	N = 20	N = 30	N = 50
S1	2,75	1,59	-3,27	-12,27
S2	1,63	1,74	0,81	-1,9
S3	0,3	0,92	0,24	-2,29

Мы провели расчеты для случая гот.

1,74 — наиболее предпочтителен для случая с 20-тью терминалами.

Этап 12: Эффективность конфигурирующих структур в диапазоне условий

{Si}	{M}				E
	P(10) = 0,1	P(20) = 0,5	P(30) = 0,3	P(50) = 0,1
S1	0,27	0,79	-0,98	-1,23	-1,15
S2	0,16	0,87	0,24	-0,19	1,08
S3	0,08	0,46	0,07	-0,23	0,38

Суммируем по строке — т.е. эффективность в данном диапазоне условий;

Умножаем вероятности на прошлую матрицу

Р(10) — т.е. вероятность подключения 10-ти терминалов

Видим, что 2-й вариант системы является предпочтительнее

Это решение дают ЛПР.

Вывод: в заданных условиях рациональной является структура S₂

↑	Оглавление
←	Лекция 18, «Методология решения слабо структуризованных проблем»	Лекция 20, «Принятие решений в процессе системного проектирования»	→