«Системный анализ и проектирование»

Е. Н. Живицкая

↑	Оглавление
←	Лекция 19, «Постановка задачи векторной оптимизации и классификация многокритериальных методов»	Лекция 21, «Современные тенденции в области системного анализа»	→

Лекция 20: Принятие решений в процессе системного проектирования

На этапе формирования облика системы определяется рациональная структура, которая подлежит дальнейшей разработке, причем этот процесс требует тесного информационного взаимодействия — представителя внешнего и внутреннего проектирования.

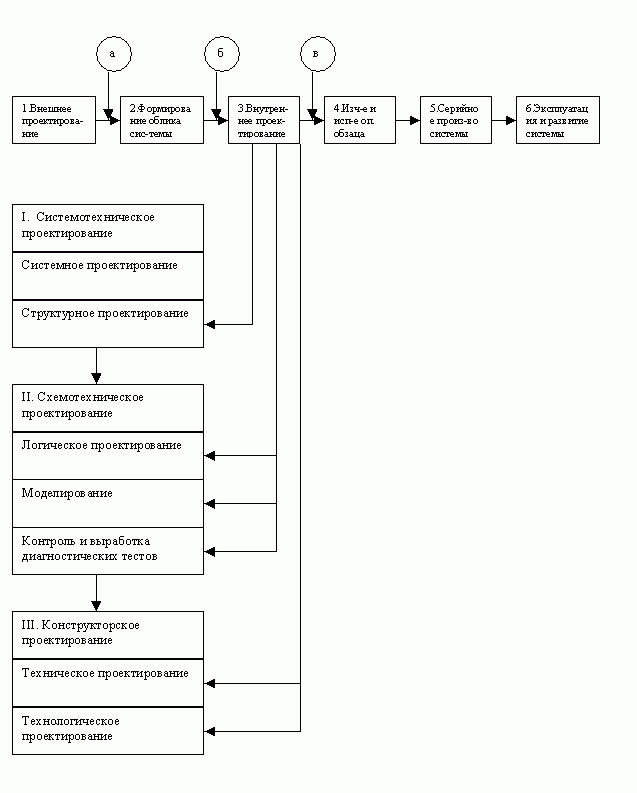
Рис. 20.1 — Схема информационного взаимодействия при формировании облика системы

а — ТЗ на проектирование системы;

б — техническое предложение на разработку системы;

в — контрольная документация на создание системы.

Сущность информационного взаимодействия при формировании облика состоит в следующем:

1. Представители внешнего проектирования разрабатывают предварительный вариант ТЗ, который содержит набор требований к системе и вектор частных критериев эффективности, определяющих систему предпочтений ЛПР.
2. На этой основе представители внутреннего проектирования выявляют исходное множество альтернативных структур, осуществляют их анализ и определяют множество конкурирующих структур, которые предъявляются ЛПР.
3. Представители внешнего проектирования решают задачу выбор рациональной структуры, уточняя свою систему предпочтений. Описание рациональной структуры и уточненный вектор частных критериев эффективности закладывается в окончательный вариант ТЗ.
4. Получив окончательный вариант ТЗ представители внутреннего проектирования составляют ТП на разработку системы, и этот документ становится основой для решения задач внутреннего проектирования.

Сущность задач системного проектирования и природа многоканальности.

Основная задача системного проектирования — это формирование структурной концепции системы без изменений детализации и пременно с увязкой требований и возможностей соответственно внешнего и внутреннего проектирования (задача формирования облика системы). По данным зарубежных источников стоимость этапа системного проектирования составляет 4% стоимости разработки системы. В то время, как стоимость решений, принятых на этом этапе составляет 70% стоимости проекта.

Отсюда следует, что ошибки системного проектирования сравнили с ошибками генерального конструктора, т.е. они, как правило, не могут быть исправлены на последующих этапах создания системы.

Задача формирования облика системы относится к классу дискретных задач векторной оптимизации. Причем, решение задачи осуществляется на фоне объективной неопределенности, которое всегда имеется в процессе раннего проектирования. Неопределенность приводит к недостаточному осознанию целевого назначения системы и следственно к нечетности в определении всех последующих атрибутов системного проектирования (основных функций системы, множества конкурирующих структур, сов-ти частных критериев и др.). Преодолевая неопределенность, важно правильно задать вектор частных критериев, так как он характеризует качество проектных решений, отражают систему предпочтений ЛПР.

Природа многокритериальности в задачах системного проектирования обусловлена следующими причинами:

1. множество технических требований, которые предъявляются к системе;
2. множество структурных элементов, входящих в состав системы;
3. множество внешних условий, в которых возможна эксплуатация системы;
4. множество типовых режимов, в которых возможна эксплуатация системы;
5. множество временных этапов, которые определяют интервал ф-я системы.

Методика сравнительной оценки 2-х структур по степени доминирования

Методика служит для выбора рациональной структуры из 2-х конкурирующих структур на основе матрицы векторных оценок [K_ji]. Методика сравнительной оценки 2-х структур включает следующие операции:

1. Конкурирующие структуры получают условное название: базовое и новое.
2. Методом экспертных оценок определяются веса частных критериев.
3. По каждому частному критерию K_j определяется степень доминирования новой структуры над базовой.
4. Полученные оценки корректируются с учетом весов.
5. Вычисляется обобщенная оценка степени доминирования новой структуры над базовой.
6. Исходя из обобщенной оценки выбирается рациональная структура.

Дадим иллюстрацию методики на конкретном примере многокритериального выбора.

{Kj}	Направление экстремума	Единицы измерения	{Si}
			S1 (базовая структура)	S2 (новая структура)
K1 — масса	min	кг	20	10
K2 — объем	min	м3	0,04	0,08
K3 — стоимость	min	тыс. руб.	5	10
K4 — память	max	Кбайт	384	512
K5 — гибкость (возможность изменения)	max	лингвистические оценки	по шкале Харингтона ОТЛ (0,9)	переводим качественнные оценки в количественные УДОВЛ (0,5)
K6 — комфортность	max	лингвистические оценки	УДОВЛ (0,5)	ОТЛ (0,9)

Таких критериев может быть 20, 30, 50 и т.д. Т.е. мы видим 2 близких структуры. Все решение «упаковываем» в таблицу:

Множество критериев {Kj}	Веса σj	Степень доминирования S2 над S1 (↑ — лучше, ↓ — хуже)	Корректировка оценок с учетом σj (↑ — лучше, ↓ — хуже)
K1	2	2↑	22↑
K2	2	0,08:0,04 = в 2 раза хуже, т.е. 2↓	22↑
K3	1	2↓	21↓
K4	3	1,3↑	1,33↑
K5	3	1,8↓	1,83↓
K6	4	1,8↑	1,84↑
Обобщенная оценка степени доминирования S2 над S1		22⋅1,33⋅1,84/(22⋅21⋅1,83) ≈ 2

В числителе — то, что лучше. В знаменателе — то, что хуже. Т.е. в 2 раза новая лучше, чем базовая.

Методика структурного анализа с использованием функций полезности

Осуществим структурную многокритериальную оптимизацию локальной ИВС, базируясь на методике структурного анализа с использованием функций полезности.

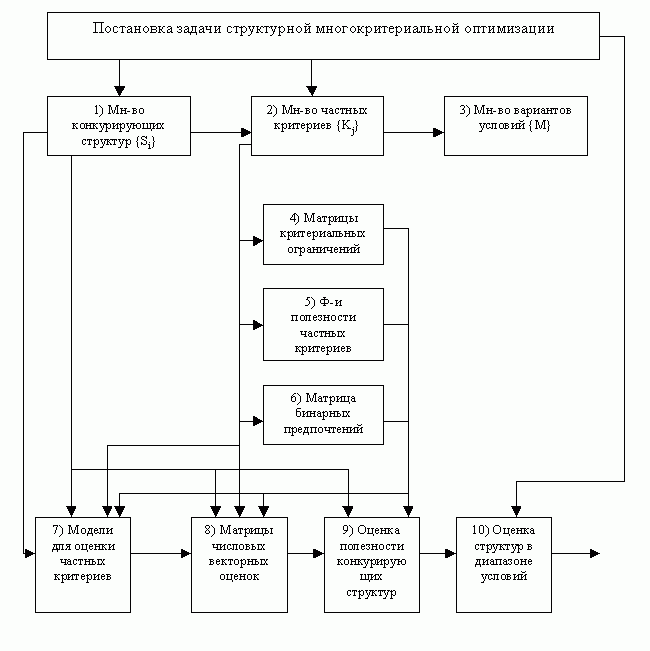
Рис. 20.2 — Структурный анализ

1. Множество конкурирующих структур {S_i}:

   S₁ — структура с одним процессором

   S₂ — структура с двумя процессорами

   S3 — структура с тремя процессорами

2. Множество частных критериев {K_j}. Пусть будет 4 частных критерия: K₁, K₂, K₃, K₄

   K₁ — время реакции системы

   K₂ — коэффициент загрузки процессора

   K₃ — пропускная способность системы

   K₄ — стоимость процессорных устройств

3. Множество вариантов условий:

   M = 1, т.е. N = 14 — пессимистическая оценка с весом 1

   M = 2, т.е. N = 17 — наиболее вероятная оценка с весом 4

   M = 3, т.е. N = 20 — оптимистическая оценка с весом 1

   т.е. вероятность этого возникновения варианта условий (1)

   P₁ = 0,17

   P₂ = 0,66

   P₃ = 0,17

4. Матрица критериальных ограничений

   {Kj}	Единицы измерения	Напр. экстр.	Худшее значение критерия	Лучшее значение критерия
   K1	сек	min	4	1
   K2	%	max	1	2
   K3	задачи/сек	max	1	2
   K4	тыс. руб.	min	800	200

5. Должны построить функции полезности

   Функции полезности частных критериев, которые используются при приведении векторных оценок к безразмерному виду.

   При этом худшее значение критерия соответствует полезности 0.

   Лучшее значение — полезности 1, а промежуточные значения подвергаются линейной апроксимации.

   Предполагается, что полезность сверх худших значениях критерия много меньше нуля. Полезность сверх лучших значений = 1.

   Графики......

6. Матрица бинарных предпочтений и соответствующие веса частных критериев

   {Kj}	K1	K2	K3	K4	σ1j веса
   K1		1	0,5	0	0,25
   K2	0		0,5	0	0,08
   K3	0,5	0,5		0	0,17
   K4	1	1	1		0,5

   Т.е. (∑ по строке)/(∑C_j)

   C_j = 1,5 + 0,5 + 1 + 3 = 2

   K₁ д.б. > K₃ (иначе не выполняется условие тр-ти).

   В реальной экспертизе получилась такая матрица. В ней есть ошибки эксперта, так как эксперт, который оаботает, может быть не последовательным. Есть правило проверки на транзированность. Если оно нарушается, следовательно эксперт допустил ошибку (а>b, b>c, следовательно a>c) (> — лучше).

7. Модели для оценки частных критериев. Для критериев K₁, K₂, K₃ используется аналитическая модель локальной ИВС. Для критерия K₄ необходимые оценки определяются расчетным путем.

8. Матрица векторных оценок для M = 1 и соответствующие веса частных критериев (т.е. к системе подключаются 14 терминов).

   {Kj}	Единицы измерения	S1	S2	S3	σ1j — вес критерия, полученный расчетным путем
   K1	сек	3,44	2,35	2,26	0,23
   K2	%	74,39	40,5	27,19	0,47
   K3	задачи/сек	1,04	1,13	1,14	0,05
   K4	тыс. руб.	340	490	640	0,25

   Матрица векторных оценок для M = 2 и соответствующие веса частных критериев

   {Kj}	Единицы измерения	S1	S2	S3	σ1j — вес критерия, полученный расчетным путем
   K1	сек	4,3	2,59	2,46	0,29
   K2	%	84,94	48,21	32,49	0,47
   K3	задачи/сек	1,19	1,35	1,36	0,07
   K4	тыс. руб.	340	490	640	0,23

   Матрица векторных оценок для M = 3 и соответствующие веса частных критериев

   {Kj}	Единицы измерения	S1	S2	S3	σ1j — вес критерия, полученный расчетным путем
   K1	сек	5,46	2,89	2,71	0,34
   K2	%	92,42	55,4	34,48	0,35
   K3	задачи/сек	1,29	1,55	1,57	0,09
   K4	тыс. руб.	340	490	640	0,22

   Вес расчитывается в результате нормировки по всем критериям

9. Оценка полезности конкурирующих структур для M = 1

   {Kj}/{Si}	S1	S2	S3	ωj
   K1	0,19	0,55	0,58	0,24
   K2	0,89	0,21	-0,6	0,27
   K3	0,04	0,13	0,14	0,11
   K4	0,77	0,52	0,27	0,38
   qiμ = 1 = ∑ωj⋅qji	0,58	0,4	0,1

   Оценка полезности конкурирующих структур для M = 2

   {Kj}/{Si}	S1	S2	S3	ωj
   K1	-1	0,47	0,51	0,21
   K2	1	0,36	0,05	0,24
   K3	0,19	0,35	0,36	0,12
   K4	0,77	0,52	0,27	0,37
   qiμ = 1 = ∑ωj⋅qji	0,28	0,45	0,29

   Оценка полезности конкурирующих структур для M = 3

   {Kj}/{Si}	S1	S2	S3	ωj
   K1	-4,9	0,37	0,43	0,29
   K2	1	0,51	0,15	0,22
   K3	0,29	0,55	0,57	0,13
   K4	0,77	0,52	0,27	0,36
   qiμ = 1 = ∑ωj⋅qji	0,89	0,48	0,33

10. Оценка полезности конкурирующих структур в диапазоне условий

    {Si}	{μ}			E = ∑qi(μ)⋅Pμ
    	S1	S2	S3
    S1	0,58	0,28	-0,89	0,13
    S2	0,4	0,45	0,48	0,45
    S3	0,1	0,29	0,33	0,26

Вывод: в заданных условиях рациональной является структура S₂.

Интерактивная процедура идентификации предпочтений ЛПР на множестве частных критериев

Наиболее простой и надежный метод идентификации предпочтений ЛПР — это парные сравнения, на основе которых возможно построить матрицу бинарных предпочтений и организовать проверку получаемой от ЛПР информации на непротиворечивость. В матрице бинарных предпочтений достаточно заполнить наддиагональную часть. Выполнив m⋅(m - 1)/2 парных сравнений. При этом предпочтения ЛПР выражаются в количественной форме с помощью следующих оценок L_ji:

• L_ji = +1 — строгое предпочтение K_j над K_i
• L_ji = +0,5 — слабое предпочтение K_j над K_i
• L_ji = 0 — безразличие в парных сравнениях
• L_ji = -0,5 — слабое предпочтение K_i над K_j
• L_ji = -1 — строгое предпочтение K_i над K_j

для всех (j,i) — т.е. для всех возможных пар из квадратной матрицы.

Проверка на непротиворечивость информации ЛПР может быть организована в виде проверок на транзитивность в триадах критериев K_j, K_i, K_l — т.е. будем рассматривать по 3 критерия. При этом триада критериев признается транзитивной, если выполниться хотя бы одно из условий:

[α_ij + α_ii - α_ji]≤0,5

[α_ij + α_ii - α_ji]⋅α_ij⋅α_ii⋅α_ji = 1

Рассмотрим процесс идентификации предпочтений ЛПР на множестве частных критериев локальной ИВС.

{K_j} = {K₁, K₂, K₃, K₄}

• K₁ — время реакции системы
• K₂ — коэффициент загрузки процессора
• K₃ — пропускная способность системы
• K₄ — ст-ть терминальных устройств

	K1	K2	K3	K4
K1		+1	0
K2			0
K3
K4

1. K₁, K₂, K₃: (L₁₂ + L₂₃ - L₁₃) = 1 и (L₁₂ + L₂₃ - L₁₃)⋅L₁₂⋅L₂₃⋅L₁₃ = 0, т.е. транзитивность нарушена, т.к. не выполняется соотношение исходное

   	K1	K2	K3	K4
   K1		+1	0
   K2			-0,5
   K3
   K4

2. K₁, K₂, K₃: (L₁₂ + L₂₃ - L₁₃) = 0,5 — т.е. транзитивность не нарушена. Процесс парных сравнений можно продолжать

   	K1	K2	K3	K4
   K1		+1	0	-0,5
   K2			-0,5	-1
   K3
   K4

3. K₁, K₂, K₄: (L₁₂ + L₂₄ - L₁₄) = 0,5 — т.е. транзитивность не нарушена. Продолжаем работу.

   	K1	K2	K3	K4
   K1		+1	0	-0,5
   K2			-0,5	-1
   K3				-1
   K4

4. K₃, K₄: (L₁₃ + L₃₄ - L₁₄) = 0,5 — т.е. транзитивность не нарушена. Мы заполни наддиагональную часть. Даже идет работа программы (под диагональю те же цифры, но знаки наоборот)

   	K1	K2	K3	K4
   K1		+1	0	-0,5
   K2	-1		-0,5	-1
   K3	0	+0,5		-1
   K4	+0,5	+1	+1

5. Транзитивная матрица бинарных предпочтений. Для вычисления весов нужно избавиться от «-». Поэтому прибавим по «1».

   	K1	K2	K3	K4
   K1		+2	1	0,5
   K2	0		0,5	0
   K3	1	+1,5		0
   K4	+1,5	+2	+2

6. Модифицированная матрица бинарных предпочтений.

Мы садимся за терминал и пытаемся заполнить матрицу парных сравнений

1. После того, как 0 система на основе транзитивности нас отбросит назад. Система «чувствует» это проверкой {*.
2. Начинаем думать и считать, что K₃ более предп., чем K₂. Транзитивность не нарушена.

Далее идет расчет по строкам и нормировка. Обработка последней матрицы позволяет выявить предпочтения ЛПР на множестве частных критериев. 3,5/12 = 0,29 0,5/12 = 0,04 2,5/12 = 0,21 5,5/12 = 0,46

Применяя методику структурного анализа, получаем более точные комплексные оценки конкурирующих структур локальной ИВС.

E₁ — обобщенная оценка в диапазоне первого структурного варианта.

E₁ = 0,07

E₂ = 0,44 — двухпроцессорный вариант

E₃ = 0,27 — трехпроцессорный вариант

Т.е. рациональной является структура S₂. Это типичная САПР-овская задача.

Методика для экспресс анализа структур при многих критериях (оперативного анализа структур)

Методика служит для проверки структур на их допустимость. На основе матрицы векторных оценок {K_ji}.

Для комплексной оценки структур используется вероятность достижения цели Z

P_i^Z=P(∏Z_ji)⇒max(i=1,n)

i — значит по какой-то i-той альтернативе, т.е. мы можем подсчитать вероятность для каждой i-той альтернативы

Z_ij — частная цель, состоящая в достижении наилучшей оценки по критерию K_j для структуры S_i.

Формула сложная, т.к. необходимо знать условные вероятности. Приведенный критерий возможно оценить с помощью неравенства:

P_i^Z≤min(P(Z_ji)), i = 1,n, j ∈ 1,m

т.е. по каждой альтернативе выписываем min вероятность. Это — верхняя граница. В абсолютном значении мы точно не знаем этот критерий, но по сравнительным оценкам можем выбрать лучшую структуру.

Приведенный критерий можно оценить с помощью неравенства *, которое определяет верхнюю оценку исходной вероятности по min вероятности цели (максимальный критерий), позволяющий выявить множество допустимых структур по max минимальных вероятностей, характеризующих наиболее слабые свойства структур.

Например, вероятность связности между 2-мя точками — например, min вероятность безотказной работы, т.е. находим самое слабое звено и его вероятность безотказной работы = вероятности безотказной работы для всей цели.

Методика для экспресс-анализа структур включает следующие процедуры:

1. Матрица векторных оценок [K_ji] приводится к безразмерному виду

   p_ji = K_ji/max(K_ji) для K_j → max, i∈1,n

   p_ji = min(K_ji)/K_ji для K_j → min, i∈1,n

2. Безразмерные оценки p_ji интерпретируются как вероятности достижения частных целей Z_ji

   [P(Zji)] =	p11	p12	...	p1n
   	p21	p22	...	p2n
   	...	...	...	...
   	pm1	pm2	...	pmn

3. Для всех структур определяются комплексные оценки:

   P_i^Z≤min{P(Z_ji)}, i = 1,n, j = 1,m

   т.е. расписывает минимальные вероятности по матрице в l.

4. Отбирается множество структур, для которых: P_i>P₀, где P₀ — некоторое пороговое значение вероятности достижения цели.

Методика скаляризации векторных оценок для ранжирования структур

Методика служит для ранжирования структур по их предпочтительности на основе матрицы векторных оценок [K_ji].

Для комплексной оценки структур используется функция штрафа.

q_i = ϑ_j/p_ji → min(i = 1,n),

где ϑ_j — веса частных критериев, исходя из разброса векторных оценок, p_ji — безразмерные векторные оценки, направленные к максимуму.

Приведенный критерий имеет смысл штрафа за возрастание разброса векторных оценок и снижения их значения, т.е. лучшей является та структура, которой соответствует меньший штраф. Методика скаляризации векторных оценок включает следующие процедуры:

1. Матрица векторных оценок K_ji приводится к безразмерному виду (см. предыдущую методику — ф-лы для p_ji):

   p_ji = K_ji/max(K_ji) для K_j → max, i∈1,n

   p_ji = min(K_ji)/K_ji для K_j → min, i∈1,n

2. Находятся веса частных критериев

   ϑ_j = Z_j/∑Z_j, j = 1,m

   здесь Z_j = [(1/n)⋅(∑[S_ji - S_ji^{^}])]/S_ji^{^}

   S_ji^{^} = ∑p_ji/p_ji

3. Формируется матрица взвешенных оценок. Вычисляем оценки

   e_ji = ϑ_j/p_ji (j =1,m, i = 1,n)

4. Для всех структур строятся комплексные оценки

   q_i = ∑l_ji, i = 1,n

5. Выполняется ранжирование структур, причем структуры располагаются в порядке возрастания штрафа на основе комплексных оценок q_i.

Отсев неперспективных структур в процессе их проверки на перспективность

Пример: рассмотрим вычислительную систему колл. поль., для которой определена матрица векторных оценок

{Kj}	Ед. изм.	Напр. экстрем.	{S3}
			S1	S2	S3	S4	S5	S6	S7	S8
K1 — время реакции с-м	сек.	min	3,29	2,28	4,71	2,91	3,09	2,22	3,23	2,26
K2 — коэффициент загрузки	%	max	48	28	58	33	43	25	47	27
K3 — пропускная способность	задач/сек.	max	0,24	0,15	0,23	0,15	0,22	0,14	0,23	0,15
K4 — вероятность правильного ответа		max	0,74	0,74	0,75	0,75	0,86	0,86	0,54	0,54
K5 — ст-ть терм. ком.	тыс. руб.	min	336	277	319	246	316	264	331	274
K6 — уровень программного обеспечения		max	0,85	0,85	0,63	0,63	0,45	0,45	0,65	0,65
K7 — уровень комф. оборудования		max	0,8	0,85	0,6	0,65	0,5	0,55	0,7	0,75

Применим методику для экспресс-анализа структур при многих критериях

{Kj}	Напр. экстрем.	S1	S2	S3	S4	S5	S6	S7	S8
K1	min	0,67	0,97	0,47	0,76	0,72	1	0,69	0,98
K2	max	0,83	0,48	1	0,57	0,74	0,43	0,81	0,46
K3	max	1	0,62	0,96	0,62	0,92	0,58	0,96	0,62
K4	max	0,86	0,86	0,87	0,87	1	1	0,63	0,63
K5	min	0,73	0,89	0,77	1	0,78	0,93	0,74	0,9
K6	max	1	1	0,74	0,74	0,53	0,53	0,76	0,76
K7	max	0,94	1	0,7	0,76	0,59	0,65	0,82	0,88
	PiZ	0,67	0,48	0,47	0,57	0,53	0,43	0,63	0,46
	P0Z = 0,5	да	нет	нет	да	да	нет	да	нет

Минимальные значения предыдущей таблицы делим на все остальные (для 1-ой строчки). Остальные по аналогии. Методика позволяет определить множество структур S₁ S₄ S₅ S₇.

Применим методику скаляризации векторных оценок для ранжирования структур.

Веса будут рассчитывать, базируясь на безразмерных векторных оценках:

p_ji = ∑4варианта/4

{Kj}	pji	Zji	ϑji
K1	0,71	0,04	0,05
K2	0,74	0,11	0,13
K3	0,87	0,15	0,18
K4	0,84	0,12	0,15
K5	0,81	0,11	0,13
K6	0,76	0,16	0,2
K7	0,78	0,13	0,16

Методика позволяет ранжировать структуры по их предпочтительности S₁ S₇ S₄ S₅.

Cji	S1	S4	S5	S7
K1	0,07	0,07	0,07	0,07
K2	0,16	0,23	0,18	0,16
K3	0,18	0,29	0,20	0,19
K4	0,17	0,17	0,15	0,24
K5	0,18	0,13	0,17	0,18
K6	0,20	0,27	0,38	0,26
K7	0,17	0,21	0,27	0,19
qi	1,13	1,37	1,42	1,29

Базируясь на результатах ранжирования возможно отобрать лишь 2 структуры S₁ и S₇, из числа которых выбирается в дальнейшем рациональная структура.

Общая характеристика локальных ИВС

Локальная ИВС реализует современную технологию комплексируя и комплексного использования информационно-вычислительных ресурсов. К числу локальных относятся сети объединений, предприятий, учреждений и институтов протяженностью до 10-15 км. На базе локальных сетей могут решаться практически все задачи, связанные с управлением пр-вом, планированием и учетом, научными исследованиями, проектированием новой техники и технологии, автоматизации пр-ва. В локальные сети могут входить все типы ЭВМ, начиная от микромашин и кончая супер ЭВМ. Причем локальные сети могут иметь связь с региональными и глобальными ИВС.

Абонентами (объекты генерир. или потребл. инф.) локальной ИВС являются:

• ЭВМ и их комплексы;
• Устройства оперативной и внешней памяти;
• Терминалы, т.е. дисплеи, графолостроители, печатные устройства;
• Телетайпы;
• Копировальные и факсиминные аппараты;
• Телевизионные камеры и мониторы;
• Телефоны и диктофоны;
• Роторы, автом. станки и тех-мы;
• Радиоприемники, телевизоры, магнитофоны и т.д.

Каждый абонент сопрягается со станцией, которая обеспечивает передачу или прием информации.

Из совокупности абонента и станции образуется абонент станции. Для оценки качества локальных ИВС служат следующие критерии:

• надежность
• производительность
• гибкость и возможность развития
• простота реализации информации

При оценке сети по этим критериям необходимо учитывать:

• размер сети
• топологию сети
• скорость передачи информации
• физическую среду, используемую для передачи информации
• используемые протоколы и методы доступа
• наличие или отсутствие упр-го узла

На основе локальной ИВС возможно решать следующие практические задачи:

• коллективное использование ЭВМ для проведения расчетов
• создание широкого спектра банков д-х и информационно-поисковых систем
• выполнение научных, проектных, конструкторских и технологических работ
• управление роботами, машинами и автоматическими станками
• передача и временное хранение информации при помощи электронной почты
• сбор, упорядочивание и хранение информации о деятельности предприятия или учреждения
• подготовка и редактирование писем, отчетов и справок
• обмен документами без выпечатывания их на бумаге
• выписывание счетов, ведение бух. и склад. Учета
• подготовка и передача чертежей, схем, рисунков, фотографий, изображая с натуры и др.

Классификация и примеры ЛИВС

ЛИВС возможно классифицировать по следующим признакам:

1. по функциональному назначению сети
2. по механизму передачи блоков д-х
3. по числу и типу используемых абонентских систем (см. рис. 20.3)

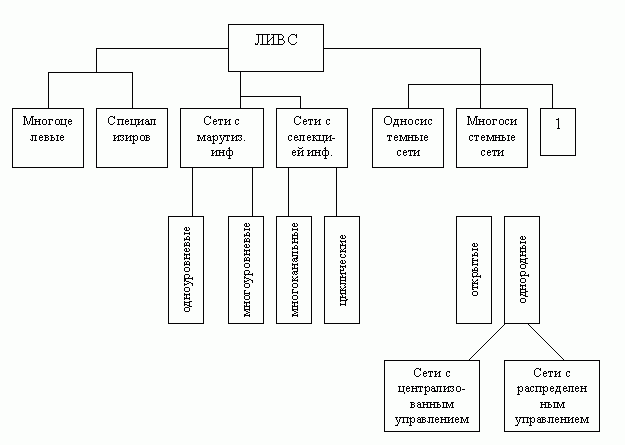
Рис. 20.3 — Классификация ЛИВС, 1 — сети персональных компьютеров

Приведем примеры иллюстрирование односистемную сеть, многосистемную сети и сеть персональных компьютеров (См. рис.1)
Коммуникационная сеть (см. рис. 2)
Сети персональных компьютеров (ПК) (см. рис.3)
ПК: персональные бытовые ЭВМ, персональные профессиональные ЭВМ (ЕС-1841), персональные вычислительные системы
Приведем пример ЛИВС, которые охватывают абонентные системы на уровне объединения (см. рис. 4)

Основные типы локальных коммуникационных сетей

Коммуникационная сеть представляет собой совокупность физической среды (эфир, световод., коксиолон., кабель, плоский кабель и др.), аппаратных и программных средств, которые обеспечивают информационную взаимосвязь между абонентами системы. С помощью интегрированных коммуникационных сетей возможно передавать в дискретной форме информацию между ЭВМ и терминами, речь человека, графические и телевизионные изображения и т.д.

Начинает появляться интеллект коммуникационной сети, позволяет подключать к сети многочисленных абонентов с нестандартным интерфейсом.

Коммуникационные сети предъявляют следующие требования:

1. высокая надежность передачи блоков данных
2. небольшая ст-ть передачи
3. высокая скорость передачи
4. износоустойчивость и долговечность оборудования
5. малые потери информации
6. минимальный штат обслуживания
7. передача данных, закодированных разным способом

Для описания коммуникационной сети используют 4 основные характеристики:

1. трафик (поток данных)
2. надежность передачи
3. время установления сквозного соединения (2-3 сеть)
4. скорость передачи блоков данных

Коммуникационные сети принято классифицировать на типы в зависимости от характера доставки блоков данных от абонента — отправителю и абонента — получателю.

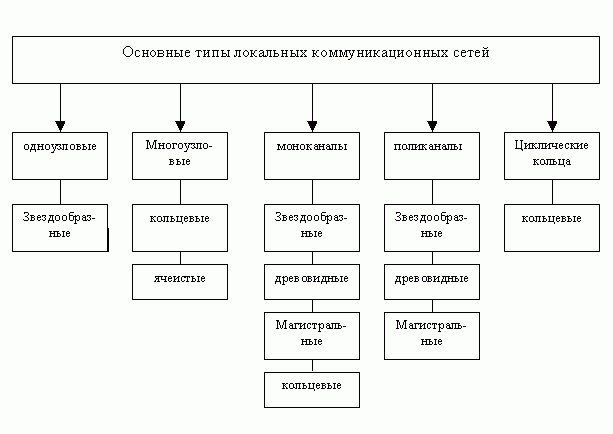
Рис. 20.4 — Коммуникационные сети

На практике широко используются моноканалы, которые имеют: звездообразную, древовидную, магистральную, кольцевую топологию.

Звездообразная топология моноканала (см. рис. 5)
Древовидный моноканал (см. рис. 6)
Магистральный моноканал (см. рис. 7)
Кольцевой моноканал (см. рис. 8)

Во всех моноканалах реализуется один и тот же принцип передачи информации. Он заключается в том, что передаваемые блоки данных принимаются почти одновременно всеми абонентами системами. После этого каждый абонент системы просматривает получаемые блоки данных, отбирает адресуемые ей блоки и уничтожает остальные.

Достоинства моноканала:

1. физическая среда полностью пассивна
2. простота прокладки моноканала
3. большая надежность моноканала
4. высокая скорость передачи информации
5. возможность одновременной передачи данных и речи
6. простота подключения новых абонентных систем

Недостатки моноканала:

1. высокая ст-ть физической среды
2. общая длина моноканала ограничена
3. относительно сложные формы управления передачей
4. сильные шумы при увеличении числа абонентских систем

Методика структурного анализа вариантов архитектуры локальной ИВС

Методика реализует начальные этапы метода комплексной оценки структур, сочетая эвристику и формализм в процессе структурного многовариантного анализа с активным использованием интерактивных процедур. Методика служит для предварительного ранжирования вариантов архитектуры локальной ИВС по вектору частных критериев и определения множества допустимых вариантов, из числа которых выбирается в дальнейшем рациональная архитектура локальной ИВС. Концептуальная схема методики:

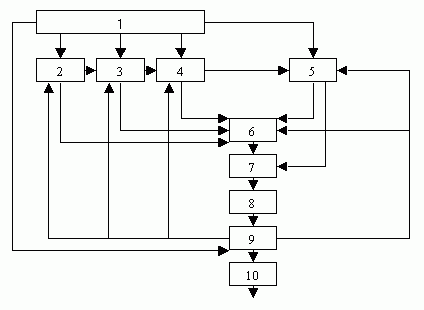
Рис. 20.5 — Варианты архитектуры локальной ИВС

Методика включает следующие основные этапы:

1. дается постановка задачи с конкретизацией целевого назначения и основных функций локальной ИВС; 2. заполняется база экспертной информации по областям применения сети, альтернативным архитектурам и частным критериям для оценки локальной ИВС;
2. определяется множество альтернативных архитектур: {A_i} = {A₁, A₂, ..., A_n}. Мы знаем 13 вариантов альтернативных архитектур;
3. определяется множество частных критериев: {K_j} = {K₁, K₂, ..., K_m};
4. формируется система предпочтений ЛПР на множестве частных критериев (оценка важности частных критериев);
5. выполняется ранжирование альтернативных архитектур по каждому из частных критериев;
6. находится результирующее ранжирование альтернативных архитектур (на основе модифицированного алгоритма Комениснелла);
7. находится усеченное множество альтернативных архитектур (на основе принципа дихотомии — «принцип вилки или поиск льва в пустыне», т.е. пустыню напополам; половину, где нет льва — отбросить, ту половину, где есть лев напополам и т.д.; ставим клетку, и лев сам в нее зайдет);
8. осуществляется анализ усеченного множества альтернативных вариантов;
9. выявляется множество допустимых вариантов архитектуры локальной ИВС, которые подвергаются дальнейшей проработке.

Пример структурного анализа вариантов архитектуры локальной ИВС

Цель структурного анализа:

Предварительное ранжирование альтернативных вариантов по вектору частных критериев и определение множества допустимых вариантов архитектуры локальной ИВС.

Этап 3: Множество альтернативных архитектур, название альтернативы:

• A₁ — полносвязная сеть
• A₂ — сеть с коммутацией пакета
• A₃ — регулярная сеть
• A₄ — нерегулярная сеть
• A₅ — иерархическая сеть
• A₆ — петлевая сеть
• A₇ — сеть с общей шиной (в произв. системах)
• A₈ — звездообразная сеть
• A₉ — петлевая сеть с переключателем
• A₁₀ — сеть с окном шины
• A₁₂ — сеть с разделяемой памятью
• A₁₃ — гибридная сеть Этап 4: Множество частных критериев
• K₁ — надежность
• K₂ — производительность
• K₃ — гибкость и возможность развития
• K₄ — простота реализации Этап 5: Идентификация предпочтений ЛПР (матрица бинарных предпочтений)

	K1	K2	K3	K4
K1		0	0,5	1
K2			0	1
K3				0,5
K4

Здесь система проверяет ошибки и заполняет нижнюю часть

Одновременно идет проверка на транзитивность

Коэффициент важности по левому критерию

KOV1 = 0,38

KOV2 = 0,33

KOV3 = 0,25

(избавиться от «-», нужно прибавить и сумму по строкам)

Этап 6: Частные ранжирования альтернативных архитектур

{Kj}	{Ai}
	A1	A2	A3	A4	A5	A6	A7	A8	A9	A10	A11	A12	A13
K1	1	2	3	4	5	6	8	7	9	10	11	10	4
K2	1	10	1	10	3	5	4	8	7	9	6	8	2
K3	10	6	10	5	4	2	1	8	4	9	3	11	7
K4	11	10	11	9	6	3	4	5	2	7	2	1	8

Т.е. мы обращаемся к базе экспертной информации за справками (есть такой блок, где находится информация по каждой альтернативе (достоинства, недостатки и т.д.)).

Этап 7: Результирующее ранжирование альтернативных архитектур

• Полная сеть
• Сеть с общей шиной
• Гибридная сеть
• Иерархическая сеть
• Петлевая сеть
• Сеть с общей шиной и переключателем
• Регулярная сеть
• Петлевая сеть с переключателем
• Звездообразная сеть
• Сеть с коммутацией пакета
• Нерегулярная сеть
• Сеть с окном шины
• Сеть с разделяемой памятью

Этап 8: Учетное множество альтернативных архитектур

• Полная сеть
• Сеть с общей шиной
• Гибридная сеть
• Иерархическая сеть
• Петлевая сеть
• Сеть с общей шиной и переключателем
• Регулярная сеть

Некоторые данные из базы экспертной информации:

A₁ — полносвязная сеть (каждый абонент непосредственно связан со всеми абонентами сети при помощи выделенных каналов связи).

Достоинства:

1. Сеть функционирует при отказах отдельных ЭВМ и каналов связи
2. Относительно высокая скорость передачи данных
3. Простота модификации и развития
4. Простота организации взаимодействия абонента
5. Очень высокая достоверность передачи информации
6. Неограниченная географическая распределенность (до 10 км)

Недостатки

1. При увеличении числа абонентов гибкость сети ухудшается
2. Увеличение числа абонентов приводит к резкому возрастанию сложности реализации и обслуживания
3. высокая стоимость зависит от числа абонентов в сети

Дополнительная информация: 1) применяется для автоматизации информационно-управляющих процессов; 2) целесообразно использовать при малом числе абонентов.

A₇ — сеть с общей шиной (абоненты взаимодействуют через моноканал в виде общей шины).Для управления доступом к шине используются специальные алгоритмы.

Достоинства:

1. Сеть устойчива к отказам отдельных ЭВМ
2. Хорошая гибкость и возможность развития
3. Простота реализации и обслуживания
4. Простота подключения новых абонентов
5. Сравнительно низкая стоимость
6. Сравнительно высокая достоверность передачи информации

Недостатки

1. Сеть не работоспособна при отказе общей шины
2. В сети могут возникнуть задержки из-за конфликтов в общей шине
3. Сквозная скорость передачи данных связана обратной зависимостью с числом элементов в сети

Дополнительная информация: 1) широко применяется практически во всех областях, наибольшее распространение получил для автоматизации управления в промышленности, автоматизации информационных управляющих процессов; 2) использование двойной общей шины позволяет резко повысить над-ть и производительность; 3) возможны очень высокие скорости передачи данных при использовании волоконно-оптического канала связи.

A₁₃ — гибридная сеть (развитие иерархической сети, в которой ЭВМ одного уровня, кроме верхнего, соединены при помощи петли или общей шины).

Достоинства:

1. сеть работоспособна при частичных отказах ЦВК (центральный вычислительный комплекс) или отказах ЭВМ на нижних уровнях. Резервирование линий связи.
2. Очень высокая производительность
3. Хорошая гибкость и возможность развития
4. Простота маршрутизации сообщений
5. Высокая достоверность передачи сообщений

Недостатки:

1. Сеть перестает работать при отказе единственной ЭВМ верхнего уровня
2. Сравнительно высокая сложность реализации и обслуживания
3. Сравнительно высокая стоимость Дополнительная информация: Прим-ся для автоматизации управления в промышленности, автоматизации информационно-управляющих процессов.

A₅ — иерархическая сеть (связи между ЭВМ образуют дерево с двумя или более уровнями. На верхнем уровне может находиться ЦВК, управляющий всей сетью).

Достоинства:

1. Сеть функционирует при частичных отказах ЦВК
2. Высокая скорость передачи данных
3. Хорошая гибкость и возможность развития
4. Простота подключения новых абонентов
5. Сравнительно низкая сложность и стоимость
6. Сравнительно высокая достоверность передачи информации
7. Неограниченная географическая распределенность (до 10 км)

Недостатки:

1. Снижение работоспособности при отказах нижних уровней. Сеть перестает функционировать при отказе единственной ЭВМ верхнего уровня
2. Увеличение количества уровней приводит к возрастанию сложности и стоимости Дополнительная информация: широко применяется при автоматизации управления в промышленности, информационно-управляющих процессах и других областях.

↑	Оглавление
←	Лекция 19, «Постановка задачи векторной оптимизации и классификация многокритериальных методов»	Лекция 21, «Современные тенденции в области системного анализа»	→